Бен Орлин - Время переменных. Математический анализ в безумном мире

Я представляю производные функций х 2и х 3(в главе X) и правило произведения (в главе XV) через рассуждения о бесконечно малых. Увы, мой новоприобретенный радикализм снова поднимает голову: если когда-то я считал этот подход противозаконным и даже аморальным, теперь полагаю, что философская выдумка, позволяющая представить dx как «бесконечно малое приращение х », – не самая высокая цена за огромную педагогическую выгоду от привнесения в процесс геометрии.

Наглядная иллюстрация: когда я впервые преподавал математический анализ, я был потрясен, обнаружив, что объем сферы (4/3 π r 3), дифференцированный по радиусу, дает ее площадь (4 π r 2). Каким образом получилось такое невероятное совпадение? В конце концов я увидел логику: дополнительное приращение радиуса добавляет к объему крошечный внешний слой, фактически равный площади поверхности. Тот факт, который я раньше воспринимал как чисто алгебраический, теперь ощущается глубоко связанным с геометрией благодаря решающему фактору – принять dx и однотипные выражения как (временно) значимые величины.

В некотором роде каноническая производная – это 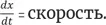Это метафора, с помощью которой я понимаю многие (или все?) другие производные. Каждый раз, когда мои ученики не могут «открыть какую-то банку», я перефразирую проблему в категориях скорости, и обычно «крышка» тут же отскакивает.

Глава о броуновском движении (гл. IX) – хорошая иллюстрация этому. Понятие дифференцируемости, если брать его абстрактно, весьма трудноуловимо. Зачем нам вообще волноваться о том, что можно дифференцировать, а что нельзя? Но в контексте кинематики «недифференцируемый» означает просто «не имеющий скорости», что передает истинную странность поведения.

Кстати, в главе III Джеймс рассуждает о том, что, если бы друзья знали все производные его счастья в данный конкретный момент, они могли бы экстраполировать траекторию счастья всей его жизни. Это предположение предугадывает существование рядов Тейлора, где в одной точке производной скрывается вся история функции.

Несколько авторов, в том числе и Джордан Элленберг, убедили меня в том, что «линеаризация» – ключевое слово математического анализа. Я также хочу признаться, что впервые наткнулся на абзацы из Твена в великолепной книге Элленберга «Как не ошибаться».

Благодаря вашему проницательному взгляду вы могли заметить, что я посвятил оптимизации четыре главы и жалкие несколько абзацев (в гл. XIV) – относительной скорости. Здесь я прошу прощения у всех ревнителей относительной скорости: я просто не нашел хороших историй о ней. А за особое внимание к оптимизации, которая является побудительной силой математического анализа, я извиняться нисколько не буду.

Хотя в главе XIII упоминается теорема Ролля, она по большей части представляет собой еще один случай оптимизации. Глава XXVI знакомит с теоремой о среднем значении одновременно для производных и интегралов; к концу в ней также обсуждается (на самом деле высмеивается) теорема о промежуточном значении. Уверен, что эта неразбериха будет раздражать добросердечных учителей, старающихся придерживаться традиционной последовательности, но такова моя точка зрения: обычный порядок изложения – это только один из возможных подходов к данному материалу, причем подход, который отдает предпочтение нарушающему исторический ход событий понятию математической строгости.

Честно говоря, не уверен, как я поступлю, когда в следующий раз буду давать этот материал. Но я планирую подчеркнуть, что теорема о среднем значении, теорема о промежуточном значении и тому подобное заняли центральное место только после работы Фурье, поднявшей значительные вопросы о сходимости и, таким образом, создавшей интеллектуальную необходимость, которую могла бы удовлетворить математическая строгость дельты и эпсилона.

Глава затрагивает несколько тем, которые заслуживают отдельного внимания: (1) экспоненциальный рост; (2) точки перегиба кривой; (3) дифференциальные уравнения. Увы, в учебном расписании эти темы часто разделяются месяцами или даже целыми семестрами, что делает эту главу довольно неудобной. Ах да, еще она показывает, что выпущенная на свободу математика не признает национальных границ.

По сравнению с производной я нахожу интегралы более коварными и неуловимыми. Фраза «область под кривой» мне кажется более ограниченной и менее честной, чем «мгновенное изменение скорости».

Таким образом, после главы XVI проходит подготовительная работа, главы XVII и XXIII исследуют некий неопределенный, метафорический интеграл. Это не слишком поможет вам справиться с домашним заданием, но, возможно, послужит абстрактным краеугольным камнем. Я считаю, что геометрические свойства интеграла, то есть то, что ∫ a bf ( x ) dx + ∫ b cg ( x ) dx = ∫ a cf ( x ) dx , в таких условиях проявляются достаточно легко.

Как учитель я подозреваю, что лучший подход к суммам Римана – очень тщательно рассчитать одну или две из них, а потом изъять их из обращения. Механизм среднеквадратичного отклонения сложен для понимания, особенно если алгебра у вас слегка хромает. Неудобство подхода заставляет искать способы обойти острые углы, что в итоге выливается в славную форму фундаментальной теоремы.

Тем не менее как писатель я решился потворствовать своей любви к анализу (возможно, вызванной тем, как мало я о нем знаю). Функция Дирихле – моя любимая: это самый простой из известных мне примеров для того, чтобы раскрыть недостатки суммы Римана и выявить необходимость интеграла Лебега. (Нельзя не признать, что она основывается на «интуитивном» знании того, что рациональные числа составляют множество нулевой меры – один из самых известных и неожиданных результатов в элементарном анализе.)