Айзек Азимов - Числа: от арифметики до высшей математики

Проанализировав числа, составляющие ряд четырехугольных чисел, мы увидим, что они тоже подчиняются определенной зависимости. Начнем с 1. Здесь нет вариантов, единица — это просто единица. Но уже 4 = 1 + 3, далее 9 = 1 + 3 + 5, 16=1+3 + 5 + 7 и так далее.

Таким образом, каждое число является суммой последовательных нечетных чисел, первое из которых единица.

Соотношение между числами треугольного и квадратного рядов показано на диаграмме.

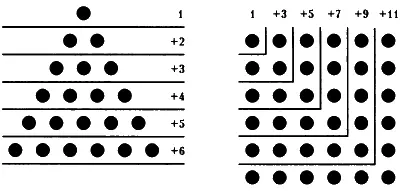
Соотношения в рядах треугольных и квадратных чисел

У греков был также ряд пентагональных чисел, которые представлены на рисунке. Этот ряд можно рассматривать как некий синтез треугольных и четырехугольных рядов. Если мы построим несколько пятиугольников таким же образом, как строили треугольники и четырехугольники, то получим числовой ряд вида 1, 5, 12, 22, 35, 51, 70 и так далее. Это ряд чисел, которые получают сложением чисел, отличающихся друг от друга на три. Первый член ряда — это единица. Второй — 5, то есть 1 + (1 + 3) = 1 + 4. Третий — 12, то есть 1 + 4 + (4 + 3) = 1 + 4 + 7, четвертый — 22, то есть 1 + 4 + 7 + 10, и так далее.

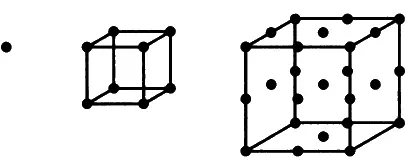
Греки изобрели и другие геометрические фигуры, моделирующие числовые ряды. Числа, составляющие такие последовательности, называются фигурными. Некоторые фигурные числа моделируются уже не плоскими фигурами, как треугольник и квадрат, а объемными, например кубами. Такие кубы трудно изобразить на рисунке, но если вы внимательно посмотрите на числовой ряд, вы сможете составить себе какое-то представление о кубической фигуре из точек. Серия кубических чисел — это ряд 1, 8, 27, 64, 125 и так далее.

Ряд кубических чисел также представляет собой ряд сумм нечетных чисел, правда, эти суммы не начинаются с единицы. Первый член ряда — это 1, второй — 8 или 3 + 5; третий — это 27 или 7 + 9 + 11; четвертый — это 64 или 13 + 15 + 17 + + 19. Каждая группа чисел, которые надо суммировать, начинается с нечетного числа, следующего за тем, которое завершало предыдущую сумму, а количество слагаемых в каждой следующей сумме на одно больше, чем в предыдущей.

Все ряды, которые мы до сих пор рассматривали, составляются при помощи повторных операций сложения. Но существуют и другие виды рядов, например ряд, который составляется при помощи повторного умножения.

Предположим, у вас есть четыре разноцветные бусины, которые надо нанизать. Сколько различных цветовых сочетаний можно составить из этих бусин?

Предположим, у нас красная, желтая, голубая и зеленая бусины (на самом деле для этого примера подошли бы любые цвета). Начать ряд можно с любого цвета, значит, у нас есть четыре возможных варианта. Выбираем одну из них, тогда нам надо нанизать еще три, следовательно, у нас есть 4x3, или 12 возможных вариантов. Осталось еще две бусины, и вы можете нанизать или одну из двух оставшихся бусин, что дает нам 4 × 3 × 2, или 24 возможных варианта. Теперь у нас осталась только одна бусина, следовательно, у нас есть 4 × 3 × 2 × 1, или 24 возможных варианта. На рисунке представлены все возможные 24 варианта цветовых комбинаций.

Мы видим, что число 24 можно представить как произведение 4 × 3 × 2 × 1. Используя такой же подход, мы можем сосчитать возможные варианты комбинаций из семи бусин различных цветов. Количество таких вариантов составляет 7 × 6 × 5 × 4 × 3 × 2 × 1, или 5040. Такой же расчет можно провести и для любого другого количества бусин.

Последовательность, составленная перемножением последовательных чисел, называется факториалом. Например, выражение «4 × 3 × 2 × 1» называется «факториал 4», по самому большому числу в этой последовательности сомножителей. Точно так же ряд 7 × 6 × 5 × 4 × 3 × 2 × 1 называется «факториал 7». Обычно для обозначения факториала используют восклицательный знак. Так, «факториал 4» — это 4!, а «факториал 7» — это 7! Использование восклицательного знака вполне обоснованно — восклицательный знак свидетельствует о том, что числа в последовательности увеличиваются очень быстро. Ряд 1!, 2!, 3!, 4! и так далее — это то же самое, что 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880 и так далее. Двадцатый член этого ряда, или 20!, равен 2 432 932 008 176 640 000.

Теперь, если мы опять вернемся к треугольным и квадратным числам, мы легко убедимся в том, что наряду с закономерными соотношениями, включающими операции сложения, существуют закономерные соотношения на основе умножения.

Вернемся в третью главу, где я рассказывал вам о том, как определить площадь квадрата. Надеюсь, вы помните, что площадь квадрата со стороной, равной 1 (например, одному сантиметру, одному метру или любой другой единицы измерения длины), равна 1 × 1, то есть единице площади, одному квадратному сантиметру, одному квадратному метру или квадрату любой другой единицы измерения длины. Площадь квадрата со стороной 2 равна 2 × 2 = 4. Теперь, если мы рассмотрим серию квадратов со сторонами, равными 1, 2, 3, 4, 5, 6, 7 и так далее, то их площади будут равны соответственно 1, 4, 9, 16, 25, 36, 49 и так далее.

Сопоставив этот ряд с теми рядами, которые мы рассматривали в предыдущих разделах этой главы, вы увидите, что перед нами ряд квадратных чисел, который записан не в прежнем виде 1, 1 + 3, 1 + 3 + 5, 16, 1 + 3 + 5 + 7 и так далее, а в виде произведения 1 × 1, 2 × 2, 3 × 3, 4 × 4, 5 × 5, 7 × 7 и так далее.

Теперь рассмотрим куб, то есть трехмерную фигуру, у которой есть длина, ширина и высота, причем все они равны между собой. Примером кубов для вас могут быть кубики для какой-нибудь настольной игры или игральные кости. Объем куба вычисляется перемножением длины, ширины и высоты. Доказать это можно с помощью той же методики, которой мы пользовались в третьей главе, вычисляя площадь квадрата или прямоугольника, когда перемножали длину и ширину.

Объем куба со стороной, равной единице, равен соответственно одной кубической единице (1 × 1 × 1 = 1). Объем куба со стороной, равной 2, равен соответственно 2 × 2 × 2 = 8, или восьми кубическим единицам. Можно продолжить такие вычисления, и тогда мы получим, что объем кубов со сторонами 1, 2, 3, 4, 5, 6, 7 и так далее равен соответственно 1, 8, 27, 64, 125, 216 и так далее. Эти числа можно представить в виде 1 × 1 × 1; 2 × 2 × 2; 3 × 3 × 3; 4 × 4 × 4; 5 × 5 × 5; 6 × 6 × 6 и так далее.

И квадраты, и кубы легко представить, так как мы часто встречаем такие фигуры в обыденной жизни. Но можно отойти от геометрических представлений и составить числовой ряд, где каждое число является произведением четырех, пяти, или шести, или любого другого количества одинаковых сомножителей.