Айзек Азимов - Числа: от арифметики до высшей математики
- Название:Числа: от арифметики до высшей математики
- Автор:
- Жанр:
- Издательство:Эксмо
- Год:2012
- Город:Москва
- ISBN:978-5-699-52723-6
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Айзек Азимов - Числа: от арифметики до высшей математики краткое содержание
Числа: от арифметики до высшей математики - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
А как обстоит дело с действительными числами? Является ли последовательность действительных чисел счетной с последовательностью целых чисел, как и последовательность всех рациональных чисел? Нет, не является. Было показано, что, как бы мы ни старались расположить действительные числа таким образом, чтобы одному действительному числу соответствовало одно целое, все равно останется бесконечное количество свободных действительных чисел.
Бесконечность действительных чисел обозначают С (от латинского «continuum»). С — это бесконечность более обширная, нежели счетная бесконечность, так как бесконечной последовательности целых чисел недостаточно, чтобы сосчитать бесконечную последовательность действительных чисел.
Можно проверить, являются ли другие виды бесконечных последовательностей счетными по отношению к бесконечной последовательности действительных чисел. Например, последовательность всех комплексных чисел (то есть все точки на плоскости, а не только точки на прямой) является счетной по отношению к последовательности всех действительных чисел. Точно так же и бесконечная последовательность гиперкомплексных чисел (то есть все точки в пространстве Вселенной, которую мы тоже считаем в данном случае бесконечной) является счетной по отношению к последовательности всех действительных чисел.
В 1896 году математик Джордж Кантор выдвинул теорию «трансфинитных чисел», согласно которой существует бесконечное количество бесконечностей разного рода. Эти бесконечности он обозначил буквой «алеф» древнееврейского алфавита. Каждую такую бесконечность обозначали при помощи правого нижнего индекса при букве «алеф»:
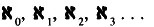
Первая бесконечность называется «алеф-ноль» и соответствует бесконечной последовательности целых чисел. Это означает, что бесконечность, с описания которой я начал эту главу, может быть самой малой из существующих бесконечностей. Другими словами, до сих пор не открыта такая бесконечная последовательность чего бы то ни было, которая не была бы счетной с последовательностью целых чисел по той причине, что остались бы лишние целые числа.
Считается, что следующая по порядку последовательность, «алеф-один» ( 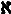 1), представляет собой С , или бесконечность континуума, но это положение еще не было доказано. Никому не удалось обнаружить бесконечной последовательности чего бы то ни было в промежутке между «алеф-ноль» (
1), представляет собой С , или бесконечность континуума, но это положение еще не было доказано. Никому не удалось обнаружить бесконечной последовательности чего бы то ни было в промежутке между «алеф-ноль» ( 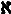 0) и С, но никто также и не доказал, что существование такой бесконечности невозможно.
0) и С, но никто также и не доказал, что существование такой бесконечности невозможно.
Бесконечность количества разнообразных кривых, которые можно нарисовать на плоскости, может быть бесконечностью «алеф-два» ( 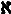 2).
2).
Что же касается следующих по порядку бесконечностей, то для них пока не было найдено соответствия.
Тем не менее уже существует концепция бесконечного разнообразия бесконечностей, которое начинается с обычной бесконечной последовательности целых чисел, наименьшей из возможных бесконечностей.
Таким образом, человек, на заре развития научившийся различать 1 и 2, путем проб и ошибок двигался к вершинам познания и в наши дни может бесстрашно оперировать такими понятиями, как многообразие бесконечностей.
В любой книге, посвященной достижениям человечества, не следует писать слово «конец», ибо конца не существует, а процесс познания бесконечен. Нужно ставить знак
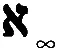
Примечания
1
Символ (+) перед положительным числом появился где-то в 1500-х годах. В те времена операцию сложения обозначали как &, например «2 плюс 3» записывали как «2&3». В скорописи значок «&» постепенно трансформировался в «φ», а потом в «+». Что же касается происхождения знака «-», то на этот счет существует множество различных теорий, но ни одна из них не кажется достаточно убедительной.
Интервал:
Закладка:










