Айзек Азимов - Числа: от арифметики до высшей математики

2 — логарифм 100,

а 100 — антилогарифм 2.

Таблица, приведенная ниже, в которой приведены антилогарифмы для ряда логарифмов, называется таблицей антилогарифмов.

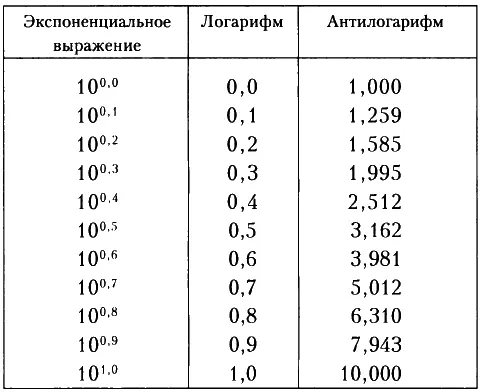
В таблице приведены приближенные значения антилогарифмов, да и невозможно привести точные значения, потому что они существуют только для таких чисел, как 10 0,0, 10 1,0и так далее. Однако величину антилогарифма можно вычислить с такой точностью (то есть до такого десятичного знака), которая требуется в данном конкретном случае.

Если мы пойдем в обратном направлении, мы можем любое число от 1 до 10 представить как 10 в какой-то степени. Другими словами, для каждого числа при помощи соответствующих методик (которые мы не будем обсуждать в нашей книжке) можно вычислить эквивалентный логарифм.

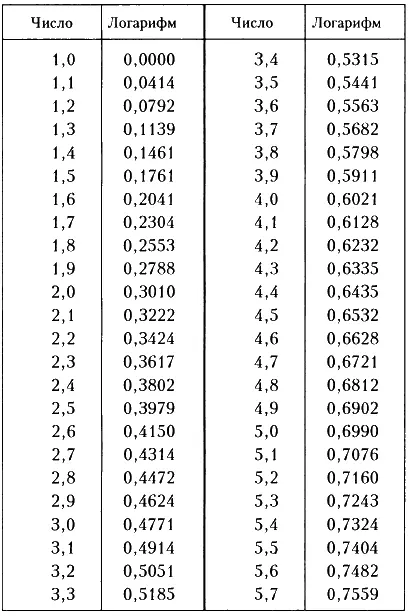
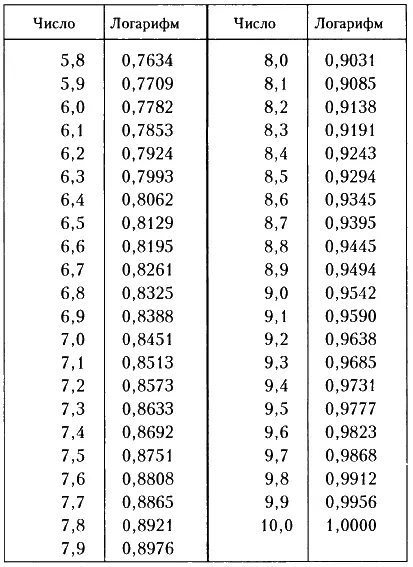
Ниже приводится краткая таблица логарифмов для ряда обычных чисел. Подробные таблицы логарифмов, в которых можно найти логарифм для любого числа, содержатся в ряде справочников.

Таблицы логарифмов уже составлены, и никому больше не нужно заниматься самостоятельными подсчетами. Эта трудоемкая работа уже проделана. Единственное, что необходимо сделать теперь, — это найти нужное значение в таблице логарифмов. Возьмем наугад какое-нибудь число, например 3,2, и найдем по таблице, приведенной ниже, значение логарифма. Логарифм 3,2 равен 0,5051. Еще один пример из таблицы: логарифм 2,4 равен 0,3802. (Разумеется, это приближенные значения логарифмов.)

Теперь, когда у нас есть значения логарифмов, то есть экспонент, можно их использовать при операциях умножения и деления.

Мы знаем, что при умножении показатели степени суммируются, значит, чтобы перемножить 3,2 и 2,4, достаточно сложить их логарифмы, 0,5051 и 0,3802, сумма которых равна 0,8853. Это пока только экспонента, то есть число, которое мы ищем, — это 10 0.8853. Теперь надо опять обратиться к таблице антилогарифмов и найти антилогарифм 0,8853. Это 7,68. Таким образом, 3,2 × 2,4 = 7,68.

Если же мы хотим поделить 3,2 на 2,4, достаточно вычесть 0,3802 из 0,5051, что равно 0,1249. Антилогарифм этого числа равен 1,333, что и является ответом.

А теперь вернемся к примеру, с которого мы начали этот раздел: 6837 × 1822. Преобразуем эти числа в экспоненциальную форму и получим (6,837 × 10 3) × (1,822 × 10 3). Логарифм 10 3— это просто 3, так как логарифм числа — это степень, в которую надо возвести 10, чтобы получить данное число. А для того чтобы получить 10 3, очевидно, надо 10 возвести в третью степень. Точно так же логарифм 10 12 равен 12, а логарифм 10 -14равен -14.

Логарифм числа 6,837 надо искать в таблице логарифмов более подробной, чем та, которая приведена в книжке. Он равен 0,83487. Тогда логарифм 6,837 × 10 3равен 0,83487 + 3 (вспомните, при перемножении чисел мы суммируем их логарифмы), или 3,83487.

Точно так же по таблице находим логарифм 1,822, который равен 0,26055, таким образом, логарифм 1,822 × 10 3равен 0,26055 + 3, или 3,26055.

Чтобы перемножить числа 6837 и 1822, нужно сложить их логарифмы, а затем найти антилогарифм суммы. Таким образом, логарифм произведения этих чисел равен 3,83487 + 3,26055, или 7,09542. Это число можно представить как 0,09542 + 7. Десятичная часть числа, в данном случае 0,09542, называется мантиссой, а целая, в данном случае 7, — характеристикой.

Антилогарифм числа — это просто число 10, возведенное в эту степень. Антилогарифм 0,09542 (определенный по таблице) равен 1,246, а антилогарифм 7 — это 10 7. При переходе от логарифма к антилогарифму сложение заменяется умножением. Таким образом, антилогарифм равен 1,246 × 10 7. Или в обычной, неэкспоненциальной форме 12 460 000.

Если вы просто перемножите 6837 на 1822 в столбик, то получите 12 457 014. Однако не следует забывать, что логарифмы — это приближенные величины, так что и результат мы можем получить только с определенным приближением.

Чтобы разделить 6837 на 1822, надо вычесть логарифм второго числа из логарифма первого, или 3,83487 — 3,26055 = 0,57432. Антилогарифм этого числа равен 3,752. Это и есть искомый ответ. Если вы выполните деление в столбик, то получите более точное выражение: 3,75192. Но как мы уже знаем, логарифмы — это приближенные величины.

Возможно, такой метод расчета показался вам громоздким и неэффективным, ведь мало того, что мы получаем приближенный результат, но надо еще искать ответы в двух таблицах. Не проще ли произвести умножение в столбик? Однако при инженерных и научных расчетах часто достаточно той точности, которую дает метод логарифмов. В то же время часто приходится проводить многократные операции деления и умножения, и метод логарифмов оказывается просто незаменим. Предположим, надо решить такой пример: (194,768 × 0,045 × 19,2 2) : (1,558 × 35,4).

Вам понадобится довольно много времени, чтобы провести все необходимые операции деления и умножения, а используя метод логарифмов, если вы хорошо освоили правила работы с логарифмическими таблицами, можно решить этот пример очень быстро. Нужно будет несколько раз заглянуть в таблицы и провести несколько операций сложения и вычитания.

Далее, если по условиям вашей задачи вам достаточно получить ответ с определенным приближением — а в инженерных и научных расчетах именно это и требуется, — метод логарифмов дает дополнительное преимущество, поскольку он значительно сокращает время, необходимое для проведения вычислений.

Ключ к сокращению времени вычислений мы найдем, если обратим внимание на характер логарифмической зависимости. Логарифм 1,0 равен 0,0000, логарифм 2,0 равен 0,3010, а логарифм 3,0 равен 0,4771. При увеличении числа от 1 до 2 величина логарифма увеличивается на 0,3010; при увеличении числа от 2 до 3 величина логарифма увеличивается на 0,1761. Логарифм 4,0 равен 0,6020, что означает увеличение на 0,1249. При увеличении числа от 9,0 до 10 логарифм увеличивается с 0,9542 до 1,0000, то есть только на 0,0458. При переходе от 19 к 20 логарифм увеличивается с 1,2788 до 1,3010, то есть только на 0,0222.

Теперь нанесем на один край линейки значения логарифмов, расположив их равномерно, а на другой край — соответствующие этим логарифмам числа (антилогарифмы).

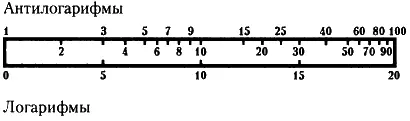
Мы видим, что обычные числа располагаются все более часто с увеличением числа. Это отражает тот факт, что с увеличением числа скорость увеличения логарифма снижается.