Айзек Азимов - Числа: от арифметики до высшей математики

Число, подобное числу 1 - i, можно представить как +1 + (-i), и оно будет на нашем шаблоне представлять собой точку пересечения прямых +1 и -i, то есть в направлении северо-запад. Точно так же -1 + i — это юго-восток, а -1 - i — это юго-запад.

Другие направления можно представить такими числами, как 15 + 2i, -7 - 3i и так далее. По сути дела, каждая точка на нашем шаблоне (который, как вы уже догадались, можно расширять бесконечно) представляет собой какое-то число, которое является суммой действительного и мнимого числа. Более того, положение точки на шаблоне может соответствовать выражению, содержащему десятичную дробь или иррациональное число, например 9,54 + 0,015i, или 2√7 + -5√2i.

Числа, подобные тем, что представлены выше, состоящие из действительной и мнимой частей, называются комплексными. Любое действительное или мнимое число может быть представлено в виде комплексного, то есть 42 = 42 + 0i, a 5i = 0 + 5i.

Комплексные числа представляют интерес не только для инженеров и ученых, они представляют и чисто практический интерес в обыденной жизни, поскольку, в отличие от обычных чисел, указывающих только величину, они указывают также и направление.

Приведем пример, который продемонстрирует вам роль комплексных чисел. Рассмотрим такое физическое понятие, как сила. Сила может представлять собой толкающее усилие или тянущее усилие. Толкающее усилие — это положительная величина, тянущее — отрицательная. Кроме того, сила может изменяться по величине. Таким образом, мы можем использовать для величины силы действительные числа.

Но, кроме того, сила может быть направлена в разных направлениях. И толкающее усилие, и тянущее усилие могут быть направлены вверх, вниз, вбок и так далее. Выразить величину силы с учетом направления можно при помощи комплексных чисел. Таким образом, число i, которое большинству людей, не связанных с математикой, представляется таинственным, но совершенно бесполезным понятием, имеет простое практическое применение. Например, в области электроники никакая математическая обработка данных невозможна без применения комплексных чисел. Величина переменного тока меняется как по величине, так и по направлению, и для ее описания необходимо использовать комплексные числа.

Комплексные числа можно складывать и вычитать по таким же правилам, как обычные числа, причем действительные и мнимые числа складываются и вычитаются отдельно. Например, если к (+2 - 4i) прибавить (-5 + 7i), то получим (-3 + 3i). Если из ( + 2 - 4i) отнять (-5 + 7i), то получим (-7 + 11i). (Это можно продемонстрировать на нашем шаблоне, так как обычное сложение и вычитание можно показать на оси север-юг. Думаю, что теперь вы сможете это сделать самостоятельно.)

Вот при умножении комплексных чисел мы столкнемся с большими трудностями, чем в случае умножения действительных чисел. При умножении 35 на 28, как я вам уже объяснил в третьей главе, мы разбиваем числа на разряды, то есть 35 = = 30 + 5, 28 = 20 + 8. Затем числа перемножаются, каждое слагаемое одной части на каждое слагаемое другой части, а результаты умножения складываются.

Точно так же производят операцию умножения с комплексными числами. Для того чтобы умножить (3 + 5i) на (6 + i), нужно составить такую схему:

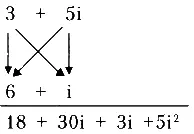
Стрелками показано, как перемножаются составные части комплексных чисел. В соответствии со схемой:

3 × 6 = 18, 3 × i = 3i, 5i × 6 = 30i и 5i × i = 5i 2= -5, поскольку i 2равно -1.

Два из промежуточных результатов являются действительными числами, и их можно сложить, то есть 18 — 5 = 13. Другие две составляющие являются мнимыми числами, и их также можно сложить: 30i + 3i = 33i. Таким образом, результатом умножения является комплексное число 13 + 33i.

Другие арифметические операции также можно продемонстрировать при помощи аналогичной схемы. Таким образом, мы видим, что с комплексными числами можно работать по тем же правилам, что и с обычными числами, а значит, комплексные числа больше не являются для нас таинственными и непостижимыми.

Область комплексных чисел дает возможность рассмотреть некоторые сложные случаи при извлечении корней степени больше 2.

Мы с вами уже знаем, что √+1 равен +1 или -1, √-1 равен + i или -i.

А чему равен корень четвертой степени из +1 ( 4√+1)? Очевидно, что (+1) × (+1) × (+1) × ( + 1) = +1, то есть +1 — это один из корней четвертой степени из +1. Точно так же (-1) × (-1) × (-1) × (-1) = +1, то есть +1 — это также один из корней четвертой степени из +1. Но мы еще не перебрали все варианты. Как насчет выражения (+i) × (+i) × (+i) × (+i)? Результат перемножения (-i) × (-i) — это -1. Следовательно, (-i) × (-i) × (-i) × (-i) = (-1) × (-1) = +1. Это означает, что +i — это третий корень четвертой степени из +1. Точно так же мы можем показать, что —i — это четвертый корень четвертой степени из +1.

Следовательно, наша задача имеет следующий ответ: ( 4√1) = +1, -1, +i, -i. Точно так же мы можем показать, что ( 4√-1) равен +√+i, -√+i, +√-i, или -√-i, то есть эта задача имеет четыре равноценных решения.

А что же такое √+i? Ответ прост. (√+i) — это такое число, которое, будучи умножено на себя самое, дает i. Поэтому (+√+i) × (+√+i) = +i Следовательно, (+√+i) × (-√+i) × (+√-i) × (-√-i) = (+ i) × (+ i) = -1.

Следовательно, (+√+i) является одним из корней четвертой степени из (-1), другими корнями являются -√+i, +√-i и -√-i.

Точно таким же образом можно показать, что любое число имеет четыре корня четвертой степени.

Мы показали, что каждое число имеет два квадратных корня и четыре корня четвертой степени. Можно предположить также, что каждое число имеет три корня третьей степени, пять корней пятой степени, шесть корней шестой степени, сорок пять корней сорок пятой степени и так далее. Это утверждение абсолютно верно, но чтобы его доказать, потребуется сложный математический аппарат, которым мы не владеем, поэтому пока примем его на веру.

Правда, мы можем проверить это утверждение для корня третьей степени. Чему, например, равен корень кубический из 1, или ( 3√+1)? Во первых, (+1) × (+1) × (+1) = +1, то есть +1 является одним из кубических корней из 1.

А чему равны остальные два? Перейдем в область отрицательных чисел.

(-1) × (-1) × (-1) = ( + 1) × (-1) = -1

Таким образом, -1 не является корнем кубическим из 1. Более того, можно показать, что ни одно действительное число, а также ни одно мнимое (будь то -i или -И), возведенное в третью степень, не дает в результате + 1.

Значит, корень всего один, а других двух просто нет?

Эти два корня существуют, но в области комплексных чисел. Я просто приведу их значения, а вы сможете проверить, чему равны эти числа, возведенные в куб. Остальные два корня кубических из + 1 — это (-1/2 + 1/2√3i) и (-1/2 - 1/2√3i). Давайте проверим это утверждение.