Айзек Азимов - Числа: от арифметики до высшей математики

Такой метод подсчета, заключающийся в сравнении последовательных рядов (один леденец против одного ребенка, или одно четное число против одного целого числа), поможет выяснить, равны ли два ряда чисел, и если они не равны, то какой ряд больше.

Напишем ряд целых чисел, а под ним ряд четных чисел:

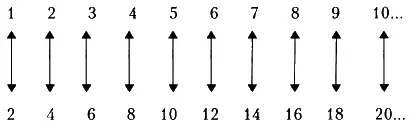
Мы видим, что для каждого целого числа нашлось четное число, причем его можно получить, умножив соответствующее целое число на 2.

Мы видим, что, как бы много чисел мы ни написали, каждому целому числу соответствует определенное четное число и, наоборот, каждому четному числу соответствует определенное целое число (то есть каждому ребенку достается по одному леденцу).

Что же это означает? Можем ли мы утверждать, что количество четных чисел равно количеству целых чисел? Не совсем так. Дело в том, что, когда речь идет о бесконечности, мы не можем сказать, что одна бесконечность равна другой бесконечности. Но мы можем утверждать, что имеется соответствие один в один между последовательностью целых чисел и последовательностью четных чисел, то есть последовательность четных чисел является взаимно однозначной с последовательностью целых чисел. Это означает, что если мы сопоставим последовательность целых чисел с последовательностью четных чисел, то для каждого целого числа найдется свое четное число и наоборот.

Точно так же мы можем сравнить последовательности целых чисел и чисел, кратных миллиону. Для каждого целого числа можно написать соответствующее число, кратное миллиону, которое мы получим умножением данного целого числа на миллион. Для 1 это будет 1 000 000, для 6 это будет 6 000 000, а для 234 — 234 000 000. То есть можно сказать, что каждому целому числу соответствует число, кратное миллиону, или что эти две последовательности соответствуют друг другу «один в один» или являются взаимно однозначными. Любая последовательность чисел, взаимно однозначная с последовательностью целых чисел, называется счетной. Последовательность целых чисел также называется счетной.

Когда речь заходит о бесконечном, в нашем воображении возникает нечто огромное и вечное, непонятное и, пожалуй, бесполезное.

Однако, даже если мы имеем дело с малыми числами, совершенно неожиданно в нашем поле зрения вновь возникает понятие «бесконечность». Предположим, нам надо разделить 1 на 1/10.Мы помним правило обратных величин и знаем, что разделить число на 1/10 это все равно что умножить его на 10. Таким образом, 1 : 1/10 = 10, 1 : 1/100 = 100, 1 : 1/1000 = 1000.

То есть чем меньше делитель при одном и том же делимом, тем больше частное от деления.

И действительно, если делить единицу или любое другое число на ряд чисел, последовательно убывающих, то есть становящихся все меньше и меньше, мы получим ряд чисел (частных от деления), которые становятся все больше и больше. А когда делитель становится бесконечно малой величиной, то частное от деления превращается в бесконечно большую величину.

Вы можете спросить: что же это такое «бесконечно малая величина»? Конечно, самой малой величиной является ноль. Но малая величина может представлять собой

дробь. Скажем, 1/10 — это малая величина, 1/100 — еще меньше, 1/1000 — еще меньше, а 1/10000 — еще меньше. Не существует предела, до которого можно уменьшать величины. Но как бы вы ни увеличивали количество нулей в знаменателе, вы никогда не достигнете нуля. Таким образом, когда вы делите единицу или какое либо другое число на последовательность бесконечно возрастающих чисел, вы получаете последовательность бесконечно убывающих чисел. Когда делитель становится бесконечно большим числом, частное становится бесконечно малым.

Обратите внимание, что мы не можем делить числа на ноль. Эта операция в математике не рассматривается, и причина очень проста. Скажем, какое частное мы получим от деления 6 на 0? Другими словами, на какое число надо умножить 0, чтобы получить 6? Такого числа нет, значит, операция 6 : 0 невозможна. Любое число, умноженное на ноль, дает ноль. Это означает, что мы не можем ни одно число разделить на ноль.

Промежуток между двумя числами, скажем, между единицей и двойкой, можно разделить на любое количество долей, на миллион, триллион и так далее, бесконечно. То же самое можно проделать и с меньшим интервалом, скажем, с интервалом между ¼ и ½ или между 0,0000001 и 0,00000001.

Математики доказали, что все возможные дроби (то есть все рациональные числа) можно расположить таким образом, чтобы получить взаимно однозначную последовательность по отношению к последовательности целых чисел.

Для каждого целого числа будет существовать соответствующая дробь, и, наоборот, не может быть дроби без соответствующего целого числа. Таким образом, последовательности всех возможных дробей являются счетными последовательностями. 

Рассмотрим бесконечную последовательность дробей:

1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, 1/512...

Обратите внимание на то, что каждая следующая дробь равна половине предыдущей, поскольку знаменатель каждый раз удваивается. (Если взять любую дробь и разделить ее на 2, например 1/128 : 2, то это то же самое, что умножить ее на 1/2, то есть 1/128 : 2 = 1/128 × 1/2, а это значит, что знаменатель удваивается.)

Хотя дроби постоянно уменьшаются, эта последовательность также является бесконечной, ведь любую сколь угодно малую дробь из этой последовательности можно разделить на два и получить еще меньшую. Знаменатель дроби увеличивается бесконечно, но сама дробь никогда не достигнет нуля, поскольку для этого надо, чтобы знаменатель достиг бесконечности, а это невозможно.

А теперь давайте выясним, чему равна сумма этой бесконечной последовательности. С точки зрения простого здравого смысла может показаться, что сумма такой последовательности должна быть бесконечно большой величиной. Но мы уже знаем, насколько обманчив бывает так называемый «здравый смысл».

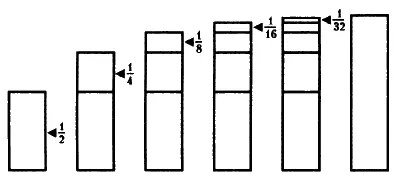
Сначала к 1/2 прибавляем 1/4, получаем 3/4, затем к 3/4 прибавляем 1/8, получаем 7/8, затем к 7/8 прибавляем 1/16, получаем 15/16, прибавляем 1/32, получаем 31/32 и так далее. Обратите внимание, что чем больше членов последовательности мы добавляем, тем ближе сумма последовательности приближается к 1. Когда мы складываем первые два члена ряда, до единицы остается 1/4, прибавляем следующий член, и до единицы остается 1/8, и так далее можно дойти до одной миллионной или до одной триллионной, но единица так никогда и не будет достигнута.

Математики так формулируют это положение: «Сумма бесконечной последовательности дробей 1/2, 1/4, 1/8… приближается к единице, которая является пределом суммы данной последовательности».