Айзек Азимов - Числа: от арифметики до высшей математики

Для чисел, меньших единицы, это правило также справедливо, за исключением деталей, касающихся экспоненциальной части. Например, рассмотрим число 0,0054. Его можно записать как 54 × 0,0001 или как 5,4 × 0,001. Каждое из этих выражений после перемножения даст один и тот же результат, 0,0054. В экспоненциальной форме это выглядит как 54 × 10 -4, 5,4 × 10 -3или 0,54 × 10 -2.

Эти выражения также эквивалентны. Как и в предыдущем примере, мы можем умножить 5,4 на 10, 10 -3разделить на 10. Деление 10 -3на 10 равноценно умножению на 10 -1. Деление равноценно вычитанию одного показателя степени из другого (-3 - 1 = -4), то есть 10 -3разделить на 10 равно 10 -3-1или 10 -4. Таким образом, мы превратили выражение 5,4 × 10 -3в 54 × 10 -4, не изменив его величины.

При помощи аналогичных процедур мы можем превратить 5,4 × 10 -3в 0,54 × 10 -2, не изменив его величины. Но на практике предпочтительнее использовать выражение 5,4 × 10 -3, поскольку в этом случае неэкспоненциальная часть находится между 1 и 10.

К экспоненциальным числам применимы те же правила, как и к обычным числам.

В операциях сложения и вычитания участвуют только неэкспоненциальные составляющие чисел. Например, при сложении 2,3 × 10 4и 4,2 × 10 4получаем 6,5 × 10 4. (Проверьте это утверждение, преобразовав экспоненциальные выражения в неэкспоненциальные: 23 000 и 42 000. Сложив их, вы получите 65 000. Такую же операцию можно осуществить со всеми примерами, которые я привел в этой главе. Таким образом, вы не только научитесь обращаться с экспоненциальными выражениями, но и на практике сможете убедиться, что не обязательно верить всему, что вам говорят, даже если это «что-то» напечатано в типографии.)

Сумма чисел 8,7 × 10 4и 3,9 × 10 4равна 12,6 × 10 4. Ответ можно оставить в этом виде, хотя неэкспоненциальная часть больше 10. Можно также при помощи операций умножения—деления, описанных выше, привести выражение к более удобному виду: 1,26 × 10 5. Этот ответ такой же правильный, как и предыдущий.

А как поступать, когда у чисел различается экспоненциальная часть? Чему будет равна сумма 1,87 × 10 4и 9 × 10 2? Для того чтобы провести сложение, потребуется привести оба числа к такому виду, когда обе экспоненциальные части одинаковы. Например, 1,87 × 10 4можно преобразовать в 187 × 10 2. Тогда можно провести сложение: (9 × 10 2) + (187 × 10 2) = (9 + 187) × 10 2 = 196 × 10 2. Можно пойти другим путем и превратить 9 × 10 2в 0,09 × 10 4, тогда получим (0,09 × 10 4) + (1,87 × 10 4) = (0,09 + 1,87) × 10 4= 1,96 × 10 4.

Таким образом, мы получили два ответа: 196 × 102 и 1,96 × 104. Эти два выражения равноценны, но использовать предпочтительно второе.

С экспоненциальными числами также можно производить операции вычитания. На практике, однако, экспоненциальной формой редко пользуются при выполнении операций сложения и вычитания, поскольку удобнее складывать и вычитать обычные числа. А вот при операциях умножения и деления экспоненциальные числа незаменимы. Предположим, надо перемножить 6000 на 0,008. Это в общем-то нетрудно сделать в столбик:

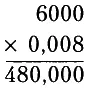
В данном примере единственную трудность представляет операция с нулями. Нужно внимательно отследить положение десятичной запятой.

А теперь попробуем провести умножение, используя экспоненциальную форму выражения чисел. Переведем числа в экспоненциальную форму: 6000 = 6 × 10 4, 0,008 = 8 × 10 -3. Перемножим эти числа: 6 × 10 4× 8 × 10 -3. 6 × 8 = 48; затем 10 4× 10 -3= 10 1. (Складываем экспоненты 4 + (-3) = 1.) Получаем ответ: 48 × 10 1, или, в более удобной форме, 48 × 10 2, или в виде обычного числа 480.

Как мы видим, используя экспоненциальную форму, мы значительно упрощаем задачу умножения, особенно в том случае, когда имеем дело с очень большими и очень маленькими числами.

Предположим, надо решить такую задачу. Сколько атомов водорода содержалось бы в Земле, если бы она состояла только из этих атомов водорода.

Масса Земли равна

6 000 000 000 000 000 000 000 000 000 грамм, а масса атома водорода — 0,00000000000000000000000166 грамма. Чтобы найти количество атомов водорода, надо массу Земли разделить на массу атома водорода, то есть разделить 6 000 000 000 000 000 000 000 000 000 на 0,00000000000000000000000166. Разумеется, вы можете проделать эту процедуру, если захотите, но, пожалуй, разумнее перейти к экспоненциальной форме.

При использовании экспоненциальных выражений задача сразу упрощается: (6 × 10 27) : (1,66 × 10 -24). Так же, как и в случае умножения, можно поделить одну неэкспоненциальную часть на другую. Таким образом, получаем частное 6 : 1,66 = 3,6 (приближенно, но достаточно для данной задачи), в то же время 10 27: 10 -24= 10 51). Таким образом, количество атомов водорода в Земле (если бы она состояла из одних атомов водорода и имела бы ту массу, которую имеет сейчас) равнялось бы 3,6 × 10 51). Или в виде обычного числа

3 600 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000

грамм, если бы просто перемножили два обычных числа, как это делали в предыдущих разделах.

Не представляет трудности также возведение в степень экспоненциальных выражений и извлечение из них корня. Так, (9 × 10 4) 2равно 9 2× (10 4) 2, что равно 81 × (10 4) 2, или 81 × 10 8, или 8,1 × 10 9. Точно так же можно извлечь корень из (9 × 10 4). Корень квадратный из (9 × 10 4) равно √9 × √10 4или 3 × 10 2.

Есть еще неясные моменты при использовании экспоненциальной формы записи чисел. Если мы имеем дело с числами с большим количеством нулей, все достаточно просто. Но предположим, что надо перемножить 6837 и 1822. Если мы запишем эти числа в экспоненциальной форме, то получим: 6,837 × 10 3и 1,822 × 10 3. Перемножить экспоненциальные части несложно, а вот что делать с числами 6,837 и 1,822? Мы столкнулись с той же задачей, как и при перемножении больших чисел, с той только разницей, что надо следить за положением десятичного знака. Другими словами, нам нужно представить число в такой форме, чтобы неэкспоненциальная часть была как можно короче или равнялась 1. Поскольку речь идет о десятеричной системе, нам понадобятся десятичные экспоненты, которые мы обсуждали в конце седьмой главы.

Теперь давайте подробнее рассмотрим экспоненты на основе 10. Начнем с 10 0= 1 и 10 1= 10. А чему равны экспоненты между 0 и 1? Например, 10 0,5= 10 ½= √10, что приблизительно равно 3,162278. Таким же способом (но с большими сложностями) можно получить значение 10 в степени от 0 до 1. Эти величины подсчитаны и собраны в специальных справочниках в виде таблиц. В нашей книжке приведена краткая таблица значений числа 10, возведенного в различные степени.

Поскольку в данном случае основанием всегда является число 10, то в таблицах обычно приводятся только показатели степени, то есть экспоненты. Отдельно записанная экспонента называется логарифмом, значение экспоненциального выражения в виде обычного числа называется антилогарифмом. Например, в выражении 10 2= 100 справедливы следующие обозначения: