Айзек Азимов - Числа: от арифметики до высшей математики

Экспоненциальная форма выражения больших чисел предоставляет два очевидных преимущества. Во-первых, такая запись очень компактна, а во-вторых, ее проще прочесть — нет необходимости считать огромное количество нулей.

Для обозначения малых чисел используют 10 в отрицательной степени. Как видно из таблицы, число 10, возведенное в отрицательные степени, представляет собой обычные числа, десятичные дроби, состоящие из определенного набора нулей, расположенных правее десятичного знака и заканчивающихся единицей. Численное значение отрицательной экспоненты равно количеству нулей после запятой плюс 1. Например, число 0,000001 имеет пять нулей после запятой, следовательно, в экспоненциальной форме оно будет записано как 10 -6.

Масса атома водорода может быть выражена в виде произведения 1,66 × 0,000000000000000000000001 грамма. (Если вы произведете операцию умножения, то получите ту величину, которая приведена в начале главы.) Второй сомножитель представляет собой 10 в отрицательной степени, оно содержит 23 нуля справа от десятичного знака. Таким образом, в экспоненциальной форме оно будет записано как 10 -24. Масса атома водорода в 1,66 раза больше этой величины, следовательно, масса водорода равна 1,66 × 10 -24.

После того как мы научились использовать числа в экспоненциальной форме на основе 10, нам будет легко разобраться в экспоненциальной форме на основе других чисел. В начале нашей книжки я уже рассказывал вам о том, что в ряде случаев удобно использовать число 12 вместо 10, поскольку у числа 12 больше множителей, чем у числа 10. (У числа 12 есть и другие преимущества, помимо большого количества сомножителей.) Древние люди определяли время по луне. Каждые 29 или 30 дней всходила новая луна и, следовательно, начинался новый месяц. Таких месяцев в году, то есть в период от одной весны до другой, было 12, точнее, 12 месяцев и 11¼ дня. Это придало числу 12 определенное магическое значение, а в древности это было очень важно для человека. Существует 12 знаков зодиака, в каждом из которых Солнце пребывает по одному месяцу при своем кажущемся вращении вокруг Земли. Число знаков зодиака нашло свое отражение и в земных делах. Это 12 племен Израиля и 12 святых апостолов.

Если мы хотим использовать 12 как основу для счетной системы, нам понадобится двенадцать разных цифр, включая ноль. Этими цифрами у нас будут 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, @ и #. Я использую символы @ и # для обозначения тех чисел, которые в десятичной системе обозначаются как 10 и 11.

Число 222 в десятеричной системе, то есть в системе, основанной на 10, можно записать как (2 × 10 2) + (2 × 10 1) + (2 × 10 0). Такое же число в двенадцатеричной системе можно перевести в десятеричную систему, записав его следующим образом: (2 × 12 2) + (2 × 12 1) + (2 × 12 0). Проведем подсчеты и получим: 288 + 24 + 2, или 314. Другими словами, число 222 в системе, основанной на 12, то есть в двенадцатеричной системе, равно числу 314 в системе, основанной на 10, то есть в десятеричной системе.

В двенадцатеричной системе число можно записать, скажем, как 3#4. Это эквивалентно (3 × 12 2) + (# × 12 1) + (4 × 12 0). Мы с вами ранее условились, что # равно 11 в десятеричной системе, следовательно, получаем 432 + 132 + 4, или 568 в десятеричной системе.

В качестве основания для системы счета можно выбрать и число меньше 10. Возьмем число 7, тогда система будет называться семеричной. Тогда нам нужно только 7 символов: 0, 1, 2, 3, 4, 5 и 6. Число 435 в семеричной системе для перевода в десятеричную можно записать как (4 × 7 2) + (3 × 7 1) + (5 × 7 0), что равно 196 + 21 + 5, или 222 в десятеричной системе.

Этот метод позволяет перевести число из одной системы счета в любую другую, причем он применим даже для десятичных дробей.

Выражение 0,15 в двенадцатеричной системе может быть представлено как (1 × 12 -1) + (5 × 12 -2), или 1/12 + 5/144, что равно 17/144 в десятеричной системе. В семеричной системе то же самое выражение можно представить как (1 × 7 -1) + (5 × 7 -2), или 1/7 + 5/49, что равно 12/49 в десятеричной системе.

Теперь давайте выясним, как определить, сколько отдельных символов необходимо для каждой отдельной системы счета. Первое число, для которого требуется два символа, — это 10 (в любой системе). Для всех чисел, меньших 10, требуются отдельные и разные символы. Все числа, большие 10, можно записать, используя комбинации символов чисел, меньших 10. Это правило, очевидно, справедливо для десятеричной системы, с которой мы так хорошо знакомы. Можно ожидать, что в других системах это правило тоже справедливо (в чем мы можем убедиться на практике).

Хорошо, теперь давайте выясним, чему равно значение выражения 10, например, в двенадцатеричной системе. Оно равно (1 × 12 1) + (0 × 12 0), или 12 + 0, или 12 в десятеричной системе. Аналогично в семеричной системе выражение 10 равно (1 × 7 1) + (0 × 7 0), или 7 + 0, или 7. Можно провести аналогичные операции и для других систем, и мы скоро убедимся, что в системе, основанной на каком-либо числе, выражение 10 соответствует именно этому числу. (В десятеричной системе 10, естественно, равно 10.)

В двенадцатеричной системе нам нужны отдельные цифры для каждого числа, меньшего 12, то есть 12 различных цифр, включая ноль. В семеричной системе нам нужны отдельные цифры для каждого числа, меньшего 7, то есть 7 различных цифр, включая ноль. Это правило справедливо для всех счетных систем. Скажем, в системе счета, основанной на 28, нам понадобятся 28 различных цифр, включая ноль.

Чтобы помочь вам глубже разобраться в этих правилах, я привожу таблицу символов для первых тридцати чисел в двенадцатеричной системе, в семеричной системе и в так хорошо нам знакомой десятеричной системе.

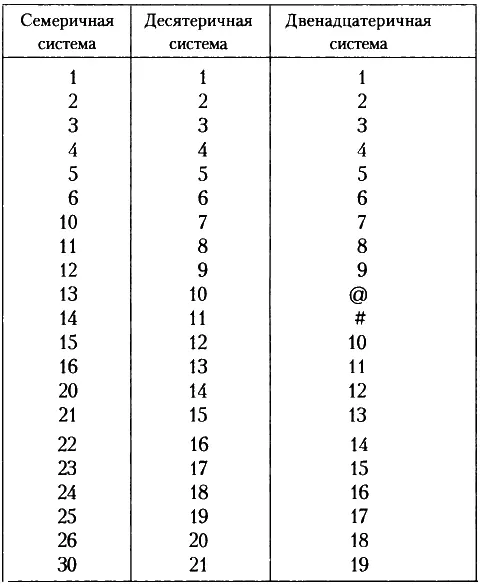
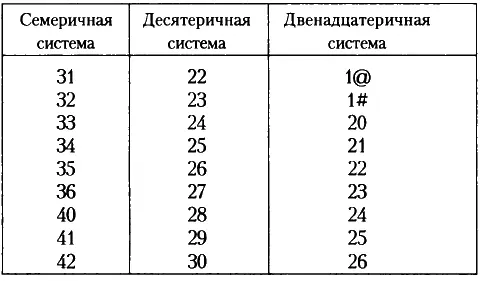
Для каждой счетной системы можно составить таблицы сложения и других арифметических действий. В двенадцатеричной системе 5 + 8 = 11, а 3 × 4 = 10. В семеричной системе 3 + 6= 12, а 5 × 3 = 21. Нам это может показаться странным, поскольку мы не используем подобные системы. Но если мы проводим все расчеты в рамках одной из таких систем, мы видим, что система также отвечает поставленным целям. Человечество остановилось на десятеричной системе по той простой причине, что на руках у человека десять пальцев, а вовсе не потому, что эта система более логична, чем любая другая.

Однако в отдельных случаях и для конкретных целей может оказаться, что какая-то система счета является гораздо более функциональной, нежели другие. Это справедливо в случае системы, основанной на 2, то есть двоичной системы.

Выражение 10 в двоичной системе равно 2 в десятеричной системе. Следовательно, в такой системе только две цифры, 0 и 1. На предыдущих страницах приведены символы для первых чисел такой системы и соответствующие эквиваленты десятеричной системы.