Бенуа Мандельброт - Фрактальная геометрия природы

Как бы то ни было, нам предстоит теперь воплотить скейлинговый принцип в действительность с тем, чтобы получить результат, отличный от броуновского движения. Для достижения этой цели я сделал весьма радикальный шаг: допустил, что приращения ln X(t+d)− ln X(t) имеет бесконечную дисперсию. До выхода в свет моих работ никто особо не задумывался при написании фразы «обозначим дисперсию через V ». О предшествующем этой фразе допущении, что величина V конечна, даже не упоминалось … и совершенно справедливо не упоминалось, поскольку нам никогда не удастся дописать до конца научную работу, если мы будем перечислять все используемые нами допущения, безотносительно к степени их «общепринятости». О причинах такой своей радикальности я расскажу позже в этом же разделе. Хотя одна из причин настолько очевидна, что о ней даже не стоит и говорить: успешное допущение V=∞ существенно облегчает для меня введение в обиход кривых бесконечной длины и поверхностей бесконечной площади.

Наблюдаемое отклонение в поведении выборочной дисперсии изменения цен.«Типичные значения», используемые для выведения итоговых данных, представляет собой наименее изощренный уровень описательной статистики, однако когда дело доходит до описания изменений цен, обычные итоговые отчеты оказываются необычайно запутанными и абсолютно ненадежными. В самом деле, используя выборочное среднее для измерения параметра сдвига, а выборочное среднеквадратическое значение – для измерения дисперсии, мы обычно руководствуемся убеждением, что эти величины представляет собой «устойчивые характеристики, которые, в конце концов, сойдутся к неким общим для всей совокупности значениям. Однако из рисунка, помещенного в моей статье [352], видно, что поведение упомянутых величин в случае цен оказывается чрезвычайно уклончивым:

А. Значения среднего квадрата, соответствующие различным длинным подвыборкам, часто имеют различный порядок величины.

Б. При увеличении размера выборки средний квадрат теряет устойчивость. Он начинает беспорядочно метаться то вверх, то вниз, при этом демонстрируя, однако, общую тенденцию к увеличению.

В. Основной вклад в величину среднего квадрата осуществляется. Как правило, всего лишь несколькими квадратами. Если удалить эти так называемые резко отклоняющиеся значения, то оценка дисперсии часто изменяется на порядок.

Гипотеза о нестационарности.Эти свойства, взятые в совокупности – как, впрочем, и любое из них в отдельности, - использовались обычно для демонстрации всем интересующимся нестационарности процесса. Мое предварительное контрпредложение заключалось в том, что сам процесс в действительности стационарен, однако при этом чрезвычайно велик неизвестный теоретический второй момент. Если допустить, что этот момент велик, но конечен, то выборочные моменты сходятся согласно закону больших чисел, однако сходятся чрезвычайно медленно, и значение предела этой сходимости не имеет практически никакой реальной ценности.

Принцип бесконечной дисперсии.Мое следующее контрпредложение заключалось в объявлении среднего квадрата совокупности бесконечным. Те читатели, кто продирался сквозь настоящее эссе с самого начала, я уверен, давно свыклись с возможностью выбора между «очень большим» и «бесконечным», однако те, кто открыл книгу именно на этом месте, возможно, пребывают в ином расположении духа, - в ином расположении духа пребывали, как выяснилось, и мои читатели в 1962 г. Всякому, кто получил обычное статистическое образование, бесконечная дисперсия представляется в лучшем случае чем-то жутковатым, а в худшем – эксцентричным. В действительности же, если «бесконечное» и отличается чем-то от «очень большого», то, судя по выборочным моментам, эту разницу заметить невозможно. Кроме того, из бесконечной дисперсии величины X никоим образом не следует, что сама величина X не может быть конечной, а ее вероятность – равной 1. Например, переменная плотности Коши 1/π(1+x 2 ) почти наверное конечна, однако имеет бесконечную дисперсию и бесконечное математическое ожидание. Таким образом, вопрос о выборе между переменными с очень большой и бесконечной дисперсией не следует решать a priori; решение должно зависеть исключительно от того, какой из вариантов окажется более удобен в данном конкретном случае. Что до меня, то я принимаю идею бесконечной дисперсии, потому что она позволяет сохранить масштабную инвариантность.

В работе [341] я сочетаю скейлинговый принцип с вполне приемлемой идеей, суть которой заключается в том, что последовательные изменения цен независимы с нулевым ожиданием; кроме того, я допускаю здесь, что дисперсия ценовых изменений бесконечна. Из краткого математического рассуждения вытекает предположение о том, что изменения цен подчиняются устойчивому распределению Леви, о котором говорится в главах 32, 33 и 39.

Это предположение оказывается справедливым в весьма широком диапазоне. В первых испытаниях [341, 352] мы применяли его ко многим товарным ценам, к некоторым процентным ставкам, а также к курсам кое-каких ценных бумаг XIX века. Позже Фама [136] подтвердил его применимость к колебаниям курсов современных ценных бумаг, а Ролл [498] – к изменениям прочих процентных ставок. Здесь же нам придется удовлетвориться одной – единственной иллюстрацией (рис. 470).

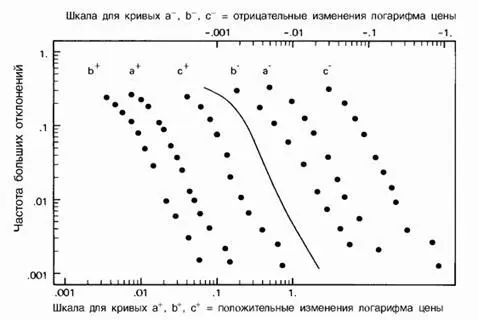
Рис. 470. Данные, подтверждающие наличие масштабной инвариантности в экономике, оригинальный вариант

К этой старой иллюстрации (которая воспроизводится здесь по [341]) я испытываю особую привязанность (несколько позднее я так же привязался к картинке, которая помещена в настоящем эссе на рис. 379). Здесь на одном графике показаны дважды логарифмические кривые положительных и отрицательных хвостов (больших отклонений) зарегистрированных изменений логарифмов цен на хлопок, а также функция совокупной плотности симметричного устойчивого распределения с показателем D=1,7 (в действительности этот показатель представляет собой несколько завышенное значение размерности D ). По ординате откладывается относительная частота случаев, когда изменение одной из определяемых ниже величин X превышало изменение абсциссы.

Скопируйте эту иллюстрацию на кальку и подвигайте ее по горизонтали. Вы обнаружите, что теоретическая кривая совпадает с любой из эмпирических кривых с точностью до незначительных отклонений общей формы. Именно такой результат и постулируется в моем скейлинговом принципе!