Бенуа Мандельброт - Фрактальная геометрия природы

В 1847 г. статью по этой теме публикует Кольрауш [273], далее следуют исследования упругого растяжения стекловолокна, предпринятые в 1865 г. Уильямом Томсоном (тем самым, который позднее стал бароном Кельвином), в 1867 г. – Джеймсом Клерком Максвеллом, и в 1874 г. – Людвигом Больцманом, статью которого Максвелл счел настолько важной, что удостоил ее упоминанием в девятом издании «Британской энциклопедии» (1878).

Над этими именами и датами стоит внимательно поразмыслить. Они свидетельствуют: для того, чтобы сделать ту или иную задачу достойной изучения, недостаточно простого проявления интереса со стороны ученых ранга Гаусса, Кельвина, Больцмана и Максвелла. Задача, которая представляется таким людям увлекательной, но в то же время оказывается им не по зубам, имеет все шансы впасть в полнейшее забвение.

Масштабная инвариантность в электростатических лейденских банках.История вопроса со слов Э. Т. Уиттекера выглядит следующим образом: «В 1745 году Питер ван Мушенбрук (1692 – 1761), профессор Лейденского университета, попытался отыскать способ предохранить электрические заряды от ослабления, какое происходило при соприкосновении заряженных тел с воздухом. С этой целью он исследовал эффект погружения электрически заряженной массы в воду, заключенную в сосуд из непроводящего материала, например, стекла. В одном из экспериментов сосуд с водой был подвешен к металлической трубке с помощью проволоки, причем проволока на несколько дюймов уходила в воду через пробку; сама же трубка, подвешенная на шелковых нитях, располагалась настолько близко от заряженного стеклянного шара, что при движении касалась его. В это время его друг по имени Кунсус, взяв стеклянный сосуд в одну руку, другой случайно коснулся металлической трубки и получил при этом сильный электрический удар; так был открыт способ накопления и усиления электрической энергии. Аббат Нолле назвал изобретенный Мушенбруком прибор лейденской склянкой».

Кольрауш [274] установил, что скорость разряда лейденской банки подчиняется той же закономерности, что и растяжение шелковых нитей: заряд уменьшается со временем по гиперболическому закону. В своей докторской диссертации Жак Кюри (брат и первый сотрудник Пьера Кюри) подробно рассмотрел поведение заряда в лейденской банке при замене стекла на другие диэлектрики и обнаружил, что одни диэлектрики дают экспоненциальное убывание заряда, другие же – гиперболическое с различными значениями показателя γ .

На протяжении более чем стандартные лет в самых различных научных журналах с завидным постоянством публиковались бесчисленные попытки объяснения масштабно-инвариантных убываний и шумов. Все эти попытки являют собой довольно жалкое зрелище. Их безуспешность однообразна и предсказуема, поскольку они снова и снова – в различных контекстах и различными словами – упираются в одни и те же тупики, бесперспективность которых была осознана еще в начале XIX в.

Панацея смеси Хопкинсона.Столкнувшись с гиперболическим убыванием заряда в лейденской банке, Хопкинсон (кстати, ученик Максвелла) выдвинул в 1878 г. «приблизительное» объяснение, основанное на том, что «стекло можно рассматривать как смесь целого ряда различных силикатов, которые ведут себя по-разному». Это надо понимать так, что функция убывания, которая выглядит как гипербола, в действительности представляет собой смесь двух или более различных экспоненциальных функций вида exp(−s/τ m ) , каждая из которых характеризуется своим значением времени релаксации τ m . Однако даже из тогдашних экспериментальных данных можно видеть, что ни двух, ни четырех экспонент недостаточно для получения гиперболической функции, и аргументацию Хопкинсона сочли несостоятельной.

И все же она продолжает время от времени всплывать, как правило, при отсутствии достаточного для ее опровержения количества данных.

Панацея распределенных значений времени релаксации.Когда данные содержат многие десятичные разряды, в результате чего эмпирическая кривая оказывается представима только в виде смеси какого-нибудь нелепого количества экспоненциальных функций (скажем, 17 или 23), возникает искушение не останавливаться на полпути и рассмотреть возможность существования смеси бесконечного числа экспоненциальных функций. Согласно определению гамма – функции Эйлера, имеем

.

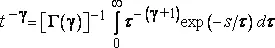Из этого тождества следует, что если «интенсивность» времени релаксации τ экспоненциальной функции равна t −(γ+1) , то смесь является гиперболической. Перед нами типичный пример логического круга. Предполагается, что на выходе научного объяснения мы должны получить нечто a priori менее очевидное, нежели имели на входе, однако в данном случае выражения t −γ и t −(γ+1) функционально идентичны.

Панацея переходного режима.Вторую по распространенности реакцию при встрече с симптомами масштабной инвариантности, описанными в предыдущем разделе, можно сформулировать следующим образом: все эти гиперболические функции t −γ объясняются, какими-либо переходными явлениями, если же наблюдать процесс убывания в течение достаточно долгого времени, то характер закономерности непременно изменится на гиперболический. Первую попытку систематического поиска «точки изменения» предпринял в 1907 г. фон Швейдлер [578]: сначала он измерял величину заряда на лейденской банке с интервалами в 100 секунд, затем интервалы постепенно становились больше, и общее время эксперимента составило 16 миллионов секунд (т.е. 200 суток – начался летом, закончился зимой!). Убывание оказалось гиперболическим, точка в точку. Позднее проводились эксперименты по измерению электрических 1/f - шумов (продолжительность опытов варьировалась от нескольких часов до нескольких дней). Результат - 1/f -убывание в поразительном большинстве случаев.

В предыдущих главах – в частности, при исследовании скоплений галактик в главе 9 – отмечалось, что ученые способны настолько погрузиться в поиски порогового значения, что их совершенно перестает занимать необходимость описания и объяснения феноменов, характерных для диапазона масштабной инвариантности. Как ни странно, инженерам также может быть свойственна чрезмерная увлеченность поисками порога, зачастую даже в большей степени. В главе 27 мы рассматривали предложенную мною модель речного стока, которую гидрологи не спешили брать на вооружение только потому, что в ней предполагается бесконечный порог масштабной инвариантности. Конечность порога в инженерном проекте не имеет абсолютно никакого значения, тем не менее, его пылко жаждут во всем остальном, казалось бы, вполне практичные люди.