Бенуа Мандельброт - Фрактальная геометрия природы

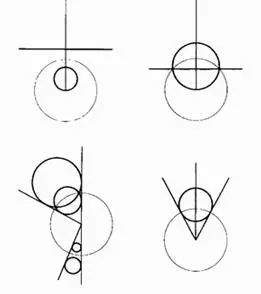
Рассмотрим теперь совокупность трех окружностей: C 1 , C 2 и C 3 . Обычно – например, когда открытые ограниченные круги, границами которых являются окружности C m , не пересекаются – существует окружность Γ , ортогональная каждой из окружностей C m . Если окружность Γ существует, она совместно самоинверсна относительно C m .

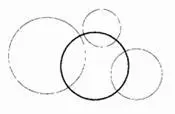
Эти краткие сведения практически исчерпывают то, что стандартная геометрия способна нам поведать о самоинверсных множествах. Остальные самоинверсные множества фрактальны, и большинство из них можно назвать какими угодно, но никак не гладкими.

Генератор. Самоинверсные множества.Как обычно, мы начинаем с генератора, который в данном случае состоит из некоторого (какого угодно) числа M окружностей C m . Преобразования, представляющие собой последовательность инверсий относительно этих окружностей, составляют то, что алгебраисты назвали бы группой, порождаемой этими инверсиями; обозначим ее буквой G . Для обозначения самоинверсного множества имеется и формальный термин: «множество, инвариантное под действием операций группы G ».

Затравки и кланы.Возьмем любое множество S (назовем его затравкой) и добавим к нему преобразования множества S под действием всех операций группы G . Результат, который мы назовем здесь кланом S , является самоинверсным. Хотя, конечно, смотреть тут особо не на что. Например, если множество S представляет собой расширенную плоскость R ⋕ (т. е. плоскость ℝ плюс точка в бесконечности), то клан S абсолютно идентичен множеству ℝ ⋕=S .

Химические инверсные группы.Кроме того, может случиться так, что при некоторой заданной группе G , основанной на инверсиях, клан каждой области S покрывает всю плоскость целиком. В этом случае самоинверсное множество также должно представлять собой всю плоскость целиком. По причинам, которые прояснятся в главе 20, я предлагаю называть такие группы хаотическими. Нехаотическими группами мы обязаны Пуанкаре, однако они носят имя Клейна: дело в том, что Пуанкаре однажды ошибочно приписал какую-то из предыдущих работ Клейна Л. Фуксу; Клейн выразил протест, и Пуанкаре в знак примирения пообещал, что назовет свое следующее великое открытие именем Клейна – и ведь назвал!

Придерживаясь пока нехаотических групп, обсудим три самоинверсных множества, отобранных еще Пуанкаре, затем еще одно множество неясного происхождения и, наконец, пятое, важность которого я обнаружил самостоятельно.

Не многим из поклонникам творчества Морица Эшера известно, что этот знаменитый рисовальщик частенько черпал вдохновение непосредственно из трудов «неизвестных» математиков и физиков (см. [89]). Вся его работа часто состояла в простом добавлении украшений к самоинверсным мозаикам, известным Пуанкаре и представленным на многочисленных иллюстрациях в [154].

Эти множества (обозначим их через T ) получаются посредством объединения кланов самих окружностей C m .

Так как группа G нехаотична, дополнением объединенных кланов окружностей C m является совокупность круговых многоугольников, называемых «открытыми плитками». Любую открытую плитку (или ее замыкание) можно трансформировать в любую другую открытую (или замкнутую) плитку посредством последовательности инверсий, принадлежащих группе G . Иными словами, клан любой замкнутой плитки есть ℝ ⋕ . Что более важно, клан любой открытой плитки есть дополнение множества T . А T является, так сказать «раствором», на который укладываются эти плитки. Плоскость ℝ ⋕ самоинверсна. Множество T и его дополнение также самоинверсны и образуют «гиперболическое разбиение» или «мозаику» на плоскости ℝ ⋕ . (Английское слово tessellation, «мозаика», происходит от латинского tessera «квадрат», которое, в свою очередь, восходит к греческому τεσσαρες «четыре», однако плитки вовсе не обязательно должны быть четырехугольными – подойдет любое число, большее 2.) А на рисунках Эшера каждая плитка украшена вдобавок причудливой картинкой.

Самым интересным самоинверсным множеством является самое маленькое. Оно называется предельным множеством (и обозначается буквой ℒ ), поскольку является также множеством предельных точек преобразований любой исходной точки под действием операций группы G . Оно принадлежит клану любой затравки S . Проясним формальное определение: множество ℒ состоит из таких предельных точек, которые не могут быть получены конечным числом инверсий. На интуитивном уровне это множество можно представить как область скопления бесконечно малых потомков.

Множество ℒ можно свести к точке или окружности, однако в общем случае оно является фрагментированным и/или/ иррегулярным фрактальным множеством.

Множество ℒ стоит в мозаике особняком, как «множество бесконечно малых плиток». Оно играет по отношению к конечным элементам мозаики такую же роль, какую играют концы ветвей (см. главу 16) по отношению к самим ветвям. Однако здесь ситуация проще: подобно ℒ мозаика T представляет собой самоинверсное множество без остатка.

Множество ℒ называется аполлониевым, если оно состоит из бесконечного количества окружностей вместе с их предельными точками. В данном случае его фрактальность является исключительно следствием фрагментации. Этот прецедент был изучен и осмыслен (хотя и в несколько многословной манере) на раннем этапе истории предмета.

Сначала мы построим основной пример, а затем покажем его самоинверсность. Аполлоний Пергский – это древнегреческий математик, живший в III в. до нашей эры. Он был представителем александрийской школы и верным последователем Евклида и известен, помимо прочего, тем, что составил алгоритм построения пяти окружностей, касательных к трем заданным окружностям. В том случае, когда заданные окружности взаимно касательны, число аполлониевых кругов равно двум. Как мы вскоре убедимся, вполне можно предположить, не потеряв при этом в общности, что две из заданных окружностей являются внешними по отношению друг к другу, но содержаться внутри третьей.