Эдвард Шейнерман - Путеводитель для влюбленных в математику

Для начала давайте представим 0,999999… не как одно число, а как ряд чисел, где каждое следующее – это предыдущее с приделанной справа цифрой 9. Вот как выглядит такой ряд:

0,9 0,99 0,999 0,9999 … (*)

и так далее ad infinitum [38] До бесконечности (лат.). – Прим. пер. . Ясно, что элементы ряда (*) постоянно возрастают. Каждый следующий элемент пусть ненамного, но больше предыдущего.

Докажем два факта:

1. Все элементы возрастающего ряда (*) меньше 1.

2. Тем не менее для любого числа x , которое меньше 1, рано или поздно отыщется элемент ряда (*), превышающий x .

Представим элементы ряда (*) в виде обыкновенных дробей:

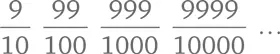
Есть компактный способ записать эти дроби. Знаменатели представляют собой степени десяти: 10 1, 10², 10³ и т. д. Каждый числитель на единицу меньше соответствующего ему знаменателя. Перепишем ряд снова:

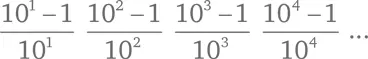
Очевидно, что n -ный элемент ряда будет выглядеть так:

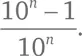
Легко убедиться, что все члены ряда (*) меньше 1, потому что числитель всякий раз оказывается меньше знаменателя.

Теперь докажем второе утверждение: если число x меньше 1, рано или поздно найдется элемент ряда (*), превышающий x .

Так как x меньше 1, разность (1 – x ) положительна. Даже если x невероятно близок к единице, разница между ними будет мизерная, но положительная. Умножим (1 – x ) на одну из степеней десяти:

10 ⁿ × (1 – x ).

Так как разность (1 – x ) положительна, это произведение будет больше 1, если 10 ⁿ достаточно велико [39] Строго говоря, это утверждение тоже надо доказать. – Прим. науч. ред. :

10 ⁿ × (1 – x ) > 1.

Раскроем скобки:

10 ⁿ – 10 ⁿx > 1,

перенесем 1 в левую часть, а 10 ⁿx в правую:

10 ⁿ – 1 > 10 ⁿx ,

поделим обе части на 10 ⁿ :

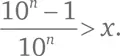
Что мы выяснили? С одной стороны, все элементы интересующего нас возрастающего ряда меньше 1. С другой стороны, какое бы число x меньше единицы мы ни взяли, рано или поздно возникнет элемент ряда, превышающий x (а последующие будут нарастать и все больше удаляться от x ).

Наш ряд неуклонно приближается к 1. Математики говорят, что этот ряд стремится к 1. Или, что то же самое, 1 представляет собой предел ряда.

Значение десятичной дроби с конечным числом символов – это сумма определенного количества десятых, сотых, тысячных и т. д. Например:

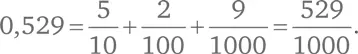
К сожалению, язык десятичных дробей с конечным числом символов слишком скуден, чтобы выразить, например, 2/7. Поэтому нам необходимо расширить лексикон.

Значение десятичной дроби с бесконечным числом символов равно пределу ряда, где на каждой ступени элемент прирастает на одну цифру. Это сложно, однако дает нам возможность выражать все числа, используя десятичную систему счисления.

Нужно приложить определенные усилия, чтобы увидеть в бесконечной десятичной дроби предел ряда. Попробуем посмотреть проще.

Вернемся к знакомому нам 0,999999… Пусть:

X = 0,999999… (A)

Умножим обе части равенства на 10:

10 X = 9,999999… (B)

Вычтем (A) из (B):

9 X = 9,000000…

Теперь поделим обе части на 9 и убедимся, что X = 1. Готово! Все оказалось просто.

Этот фокус можно повторить для любой периодической десятичной дроби. Например:

Y = 0,27272727… (C)

Умножим обе части на 100 (чтобы цифры встали в строй):

100 Y = 27,27272727… – (D)

и вычтем (C) из (D):

99 Y = 27,000000…

Таким образом, Y = 27/99 = 3/11.

Вот видите [40] Проверьте, насколько хорошо вы усвоили материал, и выразите 0,123123123123… в виде обыкновенной дроби. Ответ в конце главы. ! Зачем утруждать себя «сходимостями» и «пределами»? Но с бесконечными последовательностями нужно быть осторожнее. Представим себе сумму:

Z = 1 + 2 + 4 + 8 + 16 + 32 + … (E)

Умножим обе части равенства на 2:

2Z = 2 + 4 + 8 + 16 + 32 + … – (F)

и привычно вычтем (E) из (F):

– Z = 1.

Стало быть, Z = –1? Что за абсурд?

Где мы допустили оплошность? Мы ушли в беспредел. Алгоритм, позволяющий установить значение 0,9999999… и 0,2727272727…, дал сбой, когда мы взялись за ряд 1 + 2 + 4 + 8 + 16… Во всех трех случаях речь шла о бесконечной последовательности. В чем разница? Ответ: в сходимости. Не понимая толком, что такое сходимость ряда, мы запросто придем к выводу, что сумма положительных чисел может быть отрицательным числом. Операции с выражениями (A) и (B), а также (C) и (D) математически корректны, потому что мы имеем дело со сходящимися последовательностями.

Перед началом концерта музыканты настраивают инструменты по одной ноте, чтобы добиться гармоничного звучания. Однако это невозможно. Скоро мы увидим почему.

Целые числа прекрасно ладят с тремя простейшими арифметическими действиями – со сложением, вычитанием и умножением. Мы производим эти операции над двумя целыми числами и получаем целое же число. А вот деление одного целого числа на другое [41] Так как делить на ноль нельзя, я имею в виду такие операции, как 7/5. может привести к дробному результату.

Числа, представляющие собой результат деления целого числа на целое, называют рациональными [42] Термин «рациональные числа» происходит от латинского слова ratio, но вовсе не потому, что они, в отличие от прочих, обладают здравым смыслом. . Например, 1,5 – это рациональное число, потому что равно 3/2.

Целое число 3 рациональное, потому что 3 = 3/1 (а еще 6/2, 12/4 и т. д.). Все целые числа – рациональные.

Целые числа ладят с тремя арифметическими действиями, а рациональные числа – со всеми четырьмя. Сумма, разность, произведение и частное рациональных чисел всегда будут рациональным числом (с привычной оговоркой о неправомерности деления на ноль).

Рациональные числа пригодны для описания повседневной жизни. Величины, которые мы измеряем, – вес, интенсивность звука, расстояние, цена, температура, время, численность населения, радиочастоты – выражаются рациональными числами.

Но если рациональные числа удобны для работы и над ними можно осуществлять арифметические операции, зачем нам другие числа?