Авинаш Диксит - Стратегические игры

В главе 2мы также говорили, что незначительное изменение процедуры вычисления выигрышей позволяет обойти эту трудность. Мы сказали, что выигрыши можно измерять не в денежных суммах, а с помощью нелинейной шкалы денежных сумм. В данном приложении мы покажем, как составить такую шкалу и почему это решает нашу проблему.

Предположим, когда человек получает D долларов, мы исходим из того, что его выигрыш составляет не просто D , а, например, √ D . Тогда выигрыш от 0 долларов равен 0, а выигрыш от 100 долларов равен 10. Такое преобразование не меняет способа оценки двух выигрышей в размере 0 долларов и 100 долларов, а просто определенным образом меняет шкалу выигрышей.

Теперь проанализируем рискованную перспективу получения 100 долларов с вероятностью 0,25 и отсутствия какого бы то ни было выигрыша в противном случае. После изменения шкалы ожидаемый выигрыш (представляющий взвешенное по вероятности среднее двух выигрышей) составляет (0,75 × 0) + (0,25 × 10) = 2,5. Он эквивалентен квадратному корню из полученной денежной суммы. Поскольку 2,5 = √625, выигрыш человека, который наверняка получит 6,25 доллара, также составит 2,5. Другими словами, в случае применения шкалы выигрышей в виде квадратного корня человек был бы одинаково рад получить 6,25 доллара наверняка и 100 долларов с вероятностью 25 процентов. Подобное безразличие к гарантированным 6,25 доллара и 100 долларам в одном из четырех случаев свидетельствует о сильной нерасположенности к риску: этот человек готов пожертвовать разностью между 25 долларами и 6,25 доллара ради того, чтобы его избежать. На рис. 8П.1 показана эта нелинейная шкала (квадратный корень), ожидаемый выигрыш и безразличие человека к выбору между беспроигрышным и рискованным вариантом развития событий.

Рис. 8П.1.Вогнутая шкала: нерасположенность к риску

Но что если нелинейная шкала, используемая нами для изменения шкалы долларовых выигрышей, содержит кубический, а не квадратный корень? Тогда выигрыш от получения 100 долларов равен 4,64, а ожидаемый выигрыш от рискованного варианта составляет (0,75 × 0) + (0,25 × 4,64) = 1,16, то есть кубический корень из 1,56. Следовательно, человек с такой шкалой выигрышей наверняка получит только 1,56 доллара вместо рискованного варианта, обеспечивающего ему в среднем 25 долларов. Это означает, что у такого человека действительно очень высокий уровень нерасположенности к риску. (Для того чтобы понять, почему ситуация обстоит именно так, сравните график кубического корня из x с графиком квадратного корня из x .)

А что если изменение шкалы выигрышей, исчисляемых в x долларов, выполнить с помощью функции x 2? Ожидаемый выигрыш от рискованного варианта составит (0,75 × 0) + (0,25 × 10 000) = 2500, что равно 50 в квадрате. Стало быть, при такой шкале выигрышей человеку будет безразлично, получит ли он 50 долларов в любом случае или рискнет с ожидаемой денежной стоимостью всего 25 долларов. Этот человек должен быть склонен к риску, поскольку не желает отдавать деньги в обмен на его снижение; напротив, ему необходимо дать дополнительных 25 долларов в качестве компенсации за потерю риска. На рис. 8П.2 изображена нелинейная шкала, которой соответствует функция x 2.

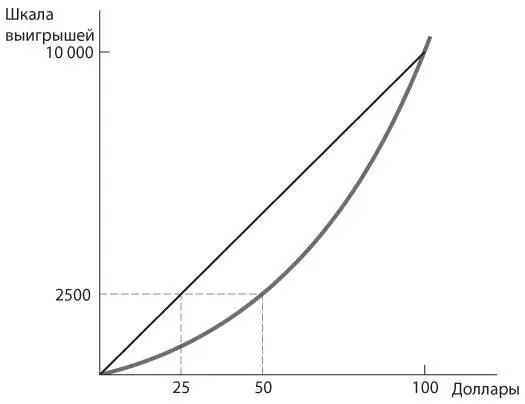
Рис. 8П.2.Выгнутая шкала: склонность к риску

Таким образом, использование разных вариантов нелинейной шкалы выигрышей вместо чистых денежных выигрышей позволяет определить разные степени неприятия риска или склонности к нему. Вогнутая шкала ( рис. 8П.1) соответствует нерасположенности к риску, а выгнутая (рис. 8П.2) — склонности к риску. Вы можете поэкспериментировать с другими простыми вариантами нелинейной шкалы (такими как логарифмы, экспоненциальные функции и другие корни и степени), чтобы выяснить, что они говорят об отношении к риску [148].

Этот метод оценки рискованных перспектив имеет давнюю традицию в теории принятия решений и обозначается термином «метод ожидаемой полезности». Нелинейная шкала, которая позволяет вычислить выигрыши как функцию денежной стоимости, называется функцией полезности; квадратный и кубический корни и квадрат — простые примеры такой функции. Математическое ожидание, или взвешенное по вероятности среднее значений полезности различных денежных сумм при случайном варианте развития событий, называется ожидаемой полезностьюэтого варианта. Различные случайные варианты сравниваются друг с другом по их ожидаемой полезности; варианты с более высокой ожидаемой полезностью считаются более приемлемыми, чем варианты с более низкой ожидаемой полезностью.

Почти вся теория игр основана на методе ожидаемой полезности, и он действительно чрезвычайно полезен, хотя и не лишен недостатков. Мы возьмем его на вооружение в данной книге, а более подробный анализ оставим для научных трудов повышенного уровня сложности [149].

Когда участники игры владеют разным объемом информации, они попытаются использовать какой-то инструмент для выяснения личной информации соперника. Как мы говорили в разделе 3данной главы, иногда непосредственная коммуникация позволяет достичь равновесия дешевого разговора. Но более типична ситуация, когда игрокам приходится определять информацию соперников посредством наблюдения за их действиями. В таком случае они должны оценить вероятность исходной информации с помощью этих действий или их наблюдаемых последствий. Такая оценка требует относительно сложных манипуляций с правилами исчисления вероятностей, и мы изучим этот процесс более подробно.

Правила вычисления вероятности событий, изложенные в приложении к главе 7, в частности правило определения комбинации вероятностей, весьма полезны для вычисления выигрышей в случаях, когда игроки располагают разным объемом информации. В играх с асимметричной информацией участники пытаются выяснить информацию, имеющуюся у соперников, посредством наблюдения за их действиями и последующих выводов (оценивания) вероятности исходной информации на основе наблюдаемых действий или их результатов.

Лучше всего это проиллюстрировать на примере. Предположим, у 1 % населения есть генетический дефект, который может вызвать определенное заболевание. Тест, позволяющий обнаружить этот дефект, имеет 99 % точности: при наличии дефекта тест не сможет его выявить в 1 % случаев, а при отсутствии может ошибочно найти в 1 % случаев. Другими словами, мы не можем непосредственно наблюдать этот дефект у человека (исходное условие), но можем наблюдать результаты теста на его наличие (последствия) — вот только тест не идеальный индикатор дефекта. В какой степени, учитывая наши наблюдения, мы можем быть уверены, что исходное условие действительно выполняется?