Авинаш Диксит - Стратегические игры

Для того чтобы ответить на этот вопрос в контексте нашего конкретного примера, мы можем произвести простые численные расчеты. Рассмотрим совокупность из 10 000 человек, в которой у 100 человек (1 %) есть дефект, а у 9900 — нет. Предположим, все они пройдут тест. Из 100 человек с дефектом тест даст правильный положительный результат у 99 человек. Из 9900 человек без дефекта тест покажет ошибочный положительный результат тоже у 99 человек. Итого будет получено 198 положительных результатов, из которых половина правильные и половина неправильные. Если человек получит положительный результат теста, это может произойти как потому, что тест действительно выявил патологию, так и по причине ошибки. Следовательно, риск того, что у человека с положительным результатом теста на самом деле есть дефект, составляет всего 50 %. (Именно поэтому тесты на обнаружение редких патологий необходимо разрабатывать так, чтобы они обеспечивали очень низкий коэффициент получения ложных положительных результатов.)

Для ответа на общие вопросы такого типа мы используем алгебраическую формулу под названием «теорема Байеса», которая позволяет поставить задачу и произвести необходимые вычисления. Для этого обобщим наш пример, допустив два варианта исходных условий, A и B (скажем, есть генетический дефект или нет), и два наблюдаемых последствия, X и Y (например, положительный или отрицательный результат теста). Предположим, что при отсутствии информации (по всей популяции) вероятность выполнения условия А равна p , а значит, вероятность выполнения условия B составляет (1 — p ). В случае выполнения условия A вероятность наблюдения X равна a , стало быть, вероятность наблюдения Y составляет (1 — a ). (В терминах, сформулированных нами в приложении к главе 7, a — это вероятность X при условии A , тогда как (1 — a ) — это вероятность Y при условии A .) Аналогичным образом при выполнении условия B вероятность наблюдения X равна b , а вероятность наблюдения Y — (1 — b ).

Это описание указывает на возможные четыре альтернативные комбинации событий: 1) выполняется A , наблюдается X ; 2) выполняется A , наблюдается Y ; 3) выполняется B , наблюдается X ; 4) выполняется B , наблюдается Y . Модифицированное правило умножения позволяет определить вероятности этих четырех комбинаций: pa, p (1 — a ), (1 — p ) b и (1 — p )(1 — b ) соответственно.

Теперь предположим, что наблюдается X : человек проходит тест на наличие генетического дефекта и получает положительный результат. Тогда мы фокусируемся на подмножестве вышеперечисленных возможностей, а именно на первой и третьей комбинации, включающих в себя наблюдение X . В этом подмножестве исходов с наблюдаемым X вероятность того, что A также выполняется, составляет pa , как показано выше. Таким образом, нам известно, с какой вероятностью мы можем наблюдать только X и с какой вероятностью — как X , так и A .

Но нас больше интересует определение вероятности того, что A выполняется при условии, что мы наблюдали X , то есть что у человека есть генетический дефект в случае положительного результата теста. Вычисление этой вероятности довольно сложное. Согласно модифицированному правилу умножения, вероятность того, что имеет место как A , так и X , равна произведению вероятности того, что имеет место X , на вероятность A при условии X . Нас интересует именно эта последняя вероятность. Воспользовавшись выведенными выше формулами для вычисления « A и X » и «только X », получим

Prob( A и X ) = Prob(только X ) × Prob( A при условии X ),

pa = [ pa + (1 — p ) b ] × Prob( A при условии X ),

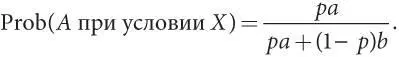
Формула дает оценку вероятности того, что A выполнялось при условии, что мы наблюдали X (и поэтому поставили все в зависимость от этого факта). Этот результат известен как теорема Байеса (а также как правило, или формула, Байеса).

В нашем примере с тестированием на наличие генетического дефекта были такие значения: Prob( A ) = p = 0,01, Prob( X при условии A ) = a = 0,99 и Prob( X при условии B ) = b = 0,01. Мы можем подставить их в формулу Байеса и получим вероятность наличия дефекта при условии положительного результата теста = Prob( A при условии X )

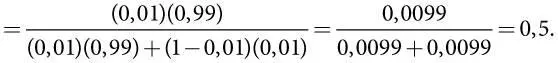
Алгебраические операции с вероятностями, проведенные с помощью правила Байеса, подтверждают результат арифметических вычислений (основанных на перечислении всех возможных случаев), которые мы использовали выше. Преимущество формулы состоит в том, что ее можно применять механически, что позволяет избежать трудоемкого и подверженного ошибкам процесса перечисления всех возможных вариантов и определения всех необходимых вероятностей.

На рис. 8П.3 правило Байеса представлено в виде таблицы, так его легче запомнить и использовать, чем формулу. В строках таблицы отображаются истинные альтернативные условия, которые могут существовать, например «генетический дефект» и «отсутствие генетического дефекта». У нас всего два варианта, A и B , но этот метод можно обобщить на любое количество возможных исходов. В столбцах таблицы отображаются наблюдаемые события — например, «положительный результат теста» и «отрицательный результат теста».

Рис. 8П.3.Правило Байеса

В каждой ячейке таблицы представлена совместная вероятность соответствующей комбинации исходного условия и наблюдения; это и есть вероятности перечисленных выше четырех комбинаций возможных вариантов. В последнем столбце справа отображена сумма по первым двум столбцам каждой из верхних двух строк. Она представляет собой общую вероятность каждого истинного условия (так, например, вероятность A равна p , как мы уже видели). В последней строке отображена сумма первых двух строк в каждом столбце. Например, запись в последней строке столбца X — это общая вероятность наблюдения X , либо когда A — истинное условие (правильный положительный результат в примере с генетическим тестом), либо когда B — истинное условие (ошибочный положительный результат).

Для того чтобы вычислить вероятность того или иного условия с учетом определенного наблюдения, согласно правилу Байеса, необходимо взять запись из ячейки, соответствующей комбинации этого условия и наблюдения, и разделить данное значение на сумму по столбцу в последней строке этого наблюдения. В качестве примера можно привести