Авинаш Диксит - Стратегические игры

a) Если бы вопрос в Исполнительном комитете решался посредством голосования по принципу большинства и все члены комитета голосовали бы в соответствии со своими предпочтениями, какой бы вариант победил?

b) Какой результат был бы получен, если бы члены Исполнительного комитета голосовали стратегически? Какого результата удалось бы достичь, если бы у одной из групп были полномочия по определению повестки дня? (Проанализируйте эти два случая в соответствии с моделью анализа, использованной в разделе 2.Би разделе 4.Б.)

S5.В книге A Mathematician Reads the Newspaper («Математик читает газету») Джон Паулос описывает следующую пародийную ситуацию, основанную на реальных событиях, произошедших во время закрытых собраний Демократической партии по выдвижению кандидата в ходе первичных выборов президента США в 1992 году. Есть пять кандидатов: Джерри Браун, Билл Клинтон, Том Харкин, Боб Керри и Пол Цонгас. Есть также 55 избирателей с разными предпочтениями в отношении кандидатов. Существует шесть разных вариантов ранжирования предпочтений, которые обозначены номерами от I до VI. Варианты ранжирования предпочтений (1 — наибольшее, 5 — наименьшее), а также количество избирателей с такими предпочтениями показаны в следующей таблице [283]:

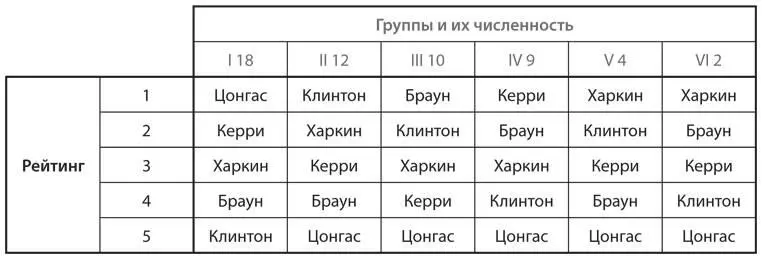
a) Сначала предположим, что все избиратели голосуют в соответствии со своими предпочтениями. Проанализируйте результаты выборов при использовании каждого из нескольких принципов голосования. Проиллюстрируйте каждый из следующих исходов: 1) при использовании метода относительного большинства голосов выигрывает Цонгас; 2) при использовании системы простого большинства со вторым туром (два кандидата, занимающих два первых места по степени предпочтений, выходят во второй тур) побеждает Клинтон; 3) при использовании метода исключения (в каждом туре кандидат с наименьшим количеством голосов за первое место исключается из списка, а остальные выходят во второй тур) победителем становится Браун; при использовании метода Кондорсе (парное сравнение) выборы выигрывает Керри.

b) Предположим, вы сторонник Брауна, Керри или Харкина. В случае голосования по принципу относительного большинства вы получите худший результат. Можете ли вы извлечь выгоду из стратегического голосования? Если да, то как именно?

c) Есть ли возможности для стратегического голосования при применении других методов? Если да, объясните, кому выгодно стратегическое голосование в каждом случае и как можно этим воспользоваться.

S6.Как упоминалось в этой главе, в целях экономии времени и денег некоторые города (такие как Сан-Франциско) вместо выборов по принципу простого большинства со вторым туром и даже первичных выборов начали использовать систему мгновенного второго тура. В большинстве административно-территориальных единиц внедрена двухэтапная система, согласно которой, если ни один кандидат не получает большинства голосов в первом туре, через несколько недель проводится второй тур с участием двух кандидатов, набравших максимальное количество голосов.

В частности, двухэтапная система применяется во Франции во время президентских выборов. Первичные выборы не проводятся. Вместо этого все кандидаты от всех партий включаются в бюллетень первого тура, что, как правило, приводит ко второму туру, поскольку одному кандидату трудно набрать большинство голосов при столь большом количестве кандидатов. Хотя второй тур президентских выборов во Франции — неизменно ожидаемое событие, это не значит, что французским выборам нечем удивлять. Так, в 2002 году вся страна была потрясена выходом кандидата от правого крыла Жан-Мари Ле Пена, обошедшего социалиста Лионеля Жоспена и занявшего второе место, во второй тур против победителя первого тура (и действующего президента) Жака Ширака. Все считали, что Жоспен займет второе место и сразится с Шираком.

Система мгновенного второго тура состоит из следующих пяти этапов:

1. Избиратели ранжируют кандидатов в соответствии со своими предпочтениями.

2. Подсчитываются голоса.

3. Если кандидат набрал большинство голосов, он побеждает в выборах. Если нет, проводится этап 4.

4. Кандидат (кандидаты) с минимальным количеством голосов исключается из списка. (Более одного кандидата исключаются из списка одновременно только в случае, если они набрали равное количество голосов.)

5. Голоса, отданные за исключенных кандидатов, переходят к кандидатам, занявшим в рейтинге следующие места. Затем процедура повторяется, начиная со второго этапа.

a) Система мгновенного второго тура постепенно набирает популярность. Она используется в ряде американских городов, а также при выборе судей в штате Северная Каролина (по состоянию на 2013 год). Учитывая потенциальную экономию времени и денег, удивляет тот факт, что она пока не получила более широкого распространения. Почему системе мгновенного второго тура оказывается противодействие? (Подсказка: каким кандидатам, партиям и заинтересованным сторонам выгодна действующая двухэтапная система?)

b) Какие опасения или критические замечания могут возникнуть по отношению к системе мгновенного второго тура?

S7.Выборы с участием трех кандидатов проходят по принципу относительного большинства. Существует множество избирателей, распределенных по шкале идеологического спектра слева направо. Представьте это распределение в виде горизонтальной прямой с двумя крайними точками: 0 (слева) и 1 (справа). Избиратели равномерно распределены по этому спектру, а значит, их количество на любом отрезке прямой пропорционально длине этого отрезка. Таким образом, треть избирателей находятся на отрезке от 0 до 1/3, четверть избирателей — на отрезке от 1/2 до 3/4 и т. д. Каждый избиратель голосует за кандидата, объявленная позиция которого ближе всего к его собственной позиции. У кандидатов нет идеологических привязанностей, поэтому они занимают любую позицию на линии, причем каждый кандидат стремится максимизировать свою долю голосов.

a) Предположим, вы один из трех кандидатов. Крайний левый из оставшихся двух расположен в точке x , а крайний правый — в точке (1 — у ), где х + у < 1 (то есть самый правый кандидат находится на расстоянии у от 1). Докажите, что ваш наилучший ответ — занять следующие позиции при заданных условиях:

(i) с небольшим смещением влево от x , если x > y и 3 x + y > 1;

(ii) с небольшим смещением вправо от (1 — y ), если y > x и x + 3 y > 1;

(iii) ровно посредине между двумя другими кандидатами, если 3 x + y < 1 и x + 3 y < 1.