Авинаш Диксит - Стратегические игры

Избиратели могут использовать стратегическое поведение в игре, которая обеспечивает выбор процедуры голосования, или в самих выборах посредством искажения своих предпочтений . Избиратели могут стратегически искажать свои предпочтения ради получения наиболее желаемого или предотвращения нежелательного результата. При наличии несовершенной информации избиратели могут принимать решение о целесообразности стратегического голосования исходя из своих убеждений в отношении поведения других избирателей и знания о распределении их предпочтений.

Кандидаты также могут придерживаться стратегического поведения в процессе формирования политической платформы. Общий результат, известный как теорема о медианном избирателе , показывает, что в выборах с участием двух кандидатов оба выбирают позицию, совпадающую с позицией предпочтений медианного избирателя . Эта теорема справедлива в случае дискретного или непрерывного распределения избирателей по шкале предпочтений.

Бинарные методы

Гистограмма

Дискретное распределение

Индекс Коупленда

Искреннее голосование

Медианный избиратель

Метод Кондорсе

Метод одобрительного голосования

Метод относительного антибольшинства

Многоэтапная процедура

Множественный метод

Непрерывное распределение

Нетранзитивное ранжирование предпочтений

Нормальное распределение

Парадокс Кондорсе

Парадокс перестановки

Парадокс повестки дня

Парное голосование

Победитель по Кондорсе

Подсчет Борда

Позиционный метод

Предпочтение с одним максимумом

Принцип минимальной дифференциации

Принцип относительного большинства голосов

Принцип простого большинства

Принцип простого большинства со вторым туром

Пропорциональное представительство

Процедура внесения поправок

Равномерное распределение

Ранжирование социальных предпочтений

Робастность

Система единого передаваемого голоса

Система мгновенного второго тура

Смешанный метод

Спойлер

Стратегическое голосование

Стратегическое искажение предпочтений

Теорема Гиббарда — Саттертуэйта

Теорема о медианном избирателе

Теорема о невозможности Эрроу

Транзитивное ранжироване предпочтений

Туры голосования

Условие Блэка

Функция распределения

Элементы Кондорсе

Элементы перестановки

S1.Рассмотрим голосование троих соседей-студентов А, Б и В, проживающих в трехместной комнате в общежитии. Они пытаются решить, какой из трех курсов выбрать для совместного изучения в этом семестре. (У всех троих разные профилирующие дисциплины и каждый изучает курсы по основному предмету.) Выбор нужно сделать из таких предметов: философия, геология и социология, а предпочтения студентов в этом отношении отражены в следующей таблице:

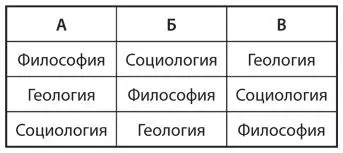
Соседи по комнате решили провести два тура голосования и будут тянуть жребий, чтобы определить, кто установит порядок голосования. Предположим, это право досталось студенту А и он хочет, чтобы выбор пал на философию. Какую повестку дня он должен установить, зная, что все будут голосовать в соответствии со своими предпочтениями во всех турах? Какой порядок голосования он должен использовать, зная, что все будут голосовать стратегически?

S2.Предположим, избирателям от 1 до 4 предлагают рассмотреть троих кандидатов (А, Б и В) в ходе выборов по методу Борда. Их предпочтения таковы:

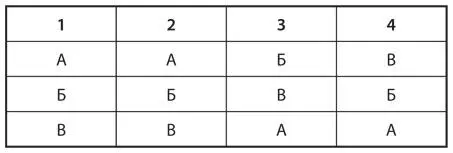
Допустим, все избиратели проголосуют в соответствии со своими предпочтениями (стратегическое голосование отсутствует). Найдите систему весов в подсчете Борда (количество баллов, которые должны быть присвоены первому, второму и третьему кандидату по уровню предпочтительности), при которой кандидат А выиграет выборы.

S3.Рассмотрите группу из 50 человек, присутствующих на собрании жителей небольшого города в штате Массачусетс. Они должны выбрать одно из трех предложений, касающихся вывоза городского мусора. Согласно предложению 1, муниципалитет сам должен обеспечивать вывоз мусора в качестве одной из услуг; предложение 2 призывает городские власти нанять для этих целей частную компанию; предложение 3 призывает жителей города самим нести ответственность за свой мусор. Существуют три типа участников голосования. Первый предпочитает предложение 1 предложению 2 и предложение 2 предложению 3; всего к этому типу относится 20 участников голосования. Второй предпочитает предложение 2 предложению 3 и предложение 3 предложению 1; к этому типу принадлежит 15 участников голосования. Третий предпочитает предложение 3 предложению 1 и предложение 1 предложению 2; таких голосующих 15.

a) Какое предложение победит в случае использования системы голосования по принципу относительного большинства?

b) Предположим, голосование проходит с применением подсчета Борда, при котором избиратели расставляют предложения в бюллетенях в порядке предпочтения. Предложение, указанное в бюллетене первым (занимает верхнюю позицию), получает 3 балла; предложение, указанное вторым, 2 балла, а указанное третьим — 1 балл. Сколько баллов в этой ситуации наберет каждое предложение при отсутствии стратегического голосования? Какое предложение победит?

c) Какую стратегию могут использовать голосующие второго и третьего типов для изменения результата голосования по методу Борда, полученного в пункте b, на результат, устраивающий оба типа? Если они применят эту стратегию, сколько баллов получит каждое предложение и какое предложение победит?

S4.Во время Карибского кризиса среди членов специально созданного Исполнительного комитета возникли серьезные разногласия. Рассматривались три варианта действий — мягкий (блокада), умеренный (ограниченный авиаудар) и жесткий (массированный авиаудар или вторжение) — между тремя группами. Гражданские «голуби мира» расположили варианты в таком порядке: мягкий курс, умеренный и жесткий. Порядок, установленный гражданскими «ястребами войны», несколько отличался: умеренный курс, жесткий и мягкий. Военные ратовали за жесткий курс, но «так хорошо понимали, какие опасности таит в себе ограниченный авиаудар, что предпочли бы вообще не предпринимать военных действий, чем прибегать к ограниченному удару» [Ernest R. May and Philip D. Zelikow, eds., The Kennedy Tapes: Inside the White House During the Cuban Missile Crisis (Cambridge, Mass.: Harvard University Press, 1997), p. 97.] Иными словами, они отдали мягкому курсу второе место, а умеренному третье. Каждая группа составляла около одной трети от общей численности Исполнительного комитета, поэтому любые две группы могли сформировать большинство.