Авинаш Диксит - Стратегические игры

Рис. 5.6.Рационализируемые стратегии

Может ли Строка исходить из убеждения, что Столбец выберет стратегию C4? В его основе должны лежать убеждения Столбца в отношении выбора Строки. Могут ли они сделать стратегию С4 наилучшим ответом Столбца? Нет. Если Столбец полагает, что Строка сыграет R2, его наилучший ответ С2. Если Столбец считает, что Строка предпочтет R3, то его наилучший ответ С3. А если Столбец убежден, что Строка выберет R4, тогда его наилучший ответ либо С1, либо С3. Следовательно, С4 не может быть наилучшим ответом Столбца [66]. Это означает, что Строка, зная о рациональности Столбца, ни в коем случае не припишет ему выбор стратегии С4. Стало быть, Строка не должна исходить из убеждения, что Столбец сыграет С4.

Обратите внимание, что хотя стратегия С4 не может быть наилучшим ответом, она не является доминируемой по отношению к стратегиям С1, С2 и С3. Для Столбца она предпочтительнее стратегии С1 против стратегии Строки R3, предпочтительнее стратегии С2 против стратегии Строки R4 и предпочтительнее стратегии С3 против стратегии Строки R1. Если стратегия все же доминируемая, она тоже не может быть наилучшим ответом. Таким образом, «стратегия, которая не может быть наилучшим ответом», — более общая концепция, чем «доминируемая стратегия». Исключение таких стратегий возможно даже тогда, когда исключение доминируемых стратегий невозможно. Следовательно, исключение стратегий, которые не могут быть наилучшим ответом, способно сузить совокупность вероятных исходов игры в большей степени, чем исключение доминируемых стратегий [67].

Исключение стратегий, которые не могут быть наилучшим ответом, также можно выполнять в итеративном режиме. Поскольку рациональный игрок Строка не может исходить из убеждения, что рациональный игрок Столбец выберет стратегию С4, рациональный игрок Столбец должен это предвидеть. Учитывая, что R4 — наилучший ответ Строки только на стратегию С4, Столбец не должен думать, что Строка сыграет R4. Следовательно, R4 и С4 не могут входить в набор рационализируемых стратегий. Концепция рационализации действительно позволяет сократить совокупность возможных исходов данной игры.

Если в игре есть равновесие Нэша, оно будет рационализируемым и его можно подтвердить посредством простой системы убеждений, состоящей из одного цикла, как в представленном выше разделе 2.В. Но в более общем плане, даже если в игре нет равновесия Нэша, она может иметь рационализируемые исходы. Возьмем в качестве примера игру два на два, полученную из игры на рис. 5.5или рис. 5.6, в которой оставлены только стратегии R1 и R3 для Строки и С1 и С3 для Столбца. Легко увидеть, что в этой игре нет равновесия Нэша в чистых стратегиях. Однако все четыре ее исхода рационализируемы посредством такой же цепочки убеждений, как выстроенная выше и охватывающая эти стратегии.

Таким образом, концепция рационализации представляет собой возможный способ решения игр с отсутствием равновесия Нэша. Что еще более важно, эта концепция подсказывает нам, как сократить совокупность вероятных исходов игры исключительно на основании рациональности.

В некоторых играх итеративное исключение стратегий, которые не могут быть наилучшим ответом, может сократить всю совокупность возможных исходов до равновесия Нэша. Обратите внимание, что мы сказали «может», а не «должно». Но если подобное все же происходит, это очень полезно, поскольку позволяет подкрепить доводы в пользу равновесия Нэша путем утверждения, что оно следует исключительно из рациональных мнений игроков о рассуждениях друг друга. Интересно, что один класс игр, решаемых таким способом, играет важную роль в экономике. К нему относится конкуренция между компаниями при определении количества производимой продукции, когда они знают, что от ее общего объема на рынке зависит цена.

Мы проиллюстрируем игру такого типа в контексте небольшого прибрежного городка. В нем две некие рыбацкие лодки каждый вечер уходят в море, а утром возвращаются с уловом и выставляют его на рынок. Игра разыгрывается во времена, когда еще не было современного холодильного оборудования, поэтому вся рыба должна быть продана и съедена в тот же день. В океане неподалеку от города полно рыбы, поэтому владелец каждой лодки может решать, сколько рыбы поймать за ночь. Но каждый из них также знает, что избыток рыбы на рынке приведет к снижению цен и прибыли.

Предположим, что если одна лодка выставит на рынок R бочек рыбы, а другая S бочек, то цена P (в дукатах за бочку) будет равна P = 60 — ( R + S ). Допустим также, что две лодки и их команды несколько отличаются по эффективности рыбной ловли: затраты первой лодки на ловлю рыбы составляют 30 дукатов на одну бочку, тогда как второй — 36 дукатов на бочку.

Теперь мы можем записать формулы определения прибыли двух владельцев лодок U и V с учетом их стратегий R и S .

U = [(60 — R — S ) — 30] R = (30 — S ) R — R 2,

V = [(60 — R — S ) — 36] S = (24 — R ) S — S 2.

На основании этих формул выигрышей можно построить кривые наилучших ответов и найти равновесие Нэша. Как и в примере игры с ценовой конкуренцией из раздела 1, выигрыш каждого игрока представляет собой квадратичную функцию его собственной стратегии при условии неизменности стратегии другого игрока. Следовательно, в данном случае можно применить математические методы, изложенные в разделе 1данной главы и в приложении к ней.

Наилучший ответ первой лодки R должен максимизировать значение U для каждого заданного значения S другой лодки. При использовании дифференциального исчисления это означает, что мы должны продифференцировать U по R при фиксированном значении S и приравнять производную к нулю, что дает следующее уравнение:

(30 — S ) — 2 R = 0; R = 15 — S / 2.

Подход без дифференциального исчисления использует результат, согласно которому значение R , максимизирующее значение U , равно R = B / (2 C ), где B = 30 — S , а C = 1. Это дает R = (30 — S ) / 2, или R = 15 — S / 2.

Аналогичным образом уравнение наилучшего ответа второй лодки можно найти, выбрав значение S , максимизирующее значение V при каждом фиксированном значении R , что дает следующее значение:

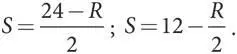
Равновесие Нэша можно найти посредством совместного решения двух уравнений наилучших ответов для R и S , что не так уж трудно сделать [68], поэтому мы просто приведем результаты. Количество: R = 12, S = 6; цена: P = 42; прибыль: U = 144, V = 36.