Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Всякий раз, когда вы преподаете двум родственникам — брату и сестре, кузенам, тете и племяннику одного возраста, вы снова и снова поражаетесь сумбурной природе биологического наследования. Я учил братьев и сестер, похожих друг на друга, словно близнецы, и близнецов, которые были совершенно не похожи друг на друга. Школьные родительские вечера всегда вносят сумятицу в мой разум. От встречи к встрече мое сознание в режиме реального времени смешивает лица матери и отца, сидящих передо мной, и я обнаруживаю, что их ребенок — безупречная работа в «Фотошопе»: его уши и ее глаза, его волосы и ее форма головы. Любые две семьи друг от друга отличаются, но в чем-то все семьи похожи.

Загадки сходства поражают биологов до глубины души [101] Статья, гораздо более заумная, чем моя глава, но все еще читабельная: Razib Khan, «Why Siblings Differ Differently», Gene Expression, Discover, February 3, 2011, http://blogs.discovermagazine.com/gnxp/2011/02/why-siblings-differ-differently/#.Wk7hKGinHOi . . Однако я не биолог, и это могут подтвердить мои ученики. У меня нет секвенатора {45} 45 Прибор для определения последовательности ДНК. — Прим. науч. ред. , нет специальных знаний об интронах и гистонах и (что еще важнее) нет даже никаких догадок на этот счет. Нет, я математик. Все, что у меня есть, — монета, теорема и — в духе «Отважного маленького тостера» {46} 46 Американский мультфильм 1987 года. — Прим. пер. — вера в силу выводов из основополагающих принципов.

И, возможно, этого достаточно.

Эта глава затрагивает два, на первый взгляд, не связанных между собой вопроса теории вероятностей. Во-первых, вопрос наследования генов, которому можно посвятить несколько школьных учебников. Во-вторых, вопрос об игре в орлянку, который кажется настолько тривиальным, что едва ли стоит наклоняться, чтобы поднять его с пола.

Можем ли мы соединить эти две области? Может ли однозвучный звон монет выразить всю сложность человеческой расы?

Я намерен ответить «да». И я вполне уверен, что унаследовал эту убежденность от отца.

Окей, начнем с простейшего из двух вопросов: что происходит, когда вы подбрасываете монету?

Ответ: есть два равновероятных исхода, орел или решка. Задача решена!

Хм, вы чувствуете это? Есть особое удовольствие в том, чтобы отвернуться от срочной, трудноразрешимой проблемы реального мира и сосредоточиться на головоломке, до которой никому нет дела. Посмакуйте это чувство. Вот почему некоторые люди становятся математиками.

Ладно, ничего особенного не происходит, если мы подбрасываем одну-единственную монету. Но что произойдет, если мы подбросим пару монет? Вы обнаружите, что равновероятны четыре исхода:

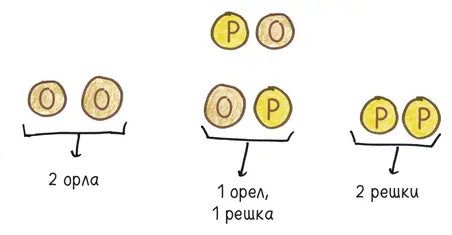
Педант сочтет, что два средних результата отличаются друг от друга: орел и решка не то же самое, что решка и орел. (Представьте, что мы подбрасываем цент и пятицентовик.) Но если вы похожи на большинство игроков в орлянку, то не увидите разницы. Ваш разум сведет оба исхода к одному (один орел, одна решка), и вероятность такого исхода — 50 %.

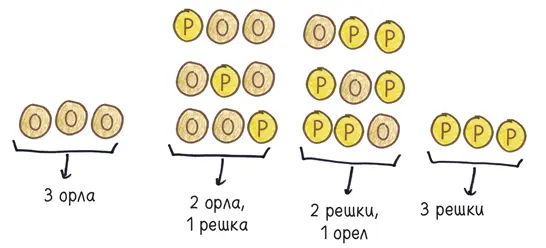
Продолжим: что произойдет, если мы подбросим три монеты?

В общей сложности восемь исходов. Если вы надеетесь, что орел выпадет трижды, есть всего один вариант: каждая монета должна выполнить свой долг, поэтому вероятность этого исхода равна 1 к 8. Но если вы надеетесь на то, что орел выпадет два раза, а решка — один, то есть три варианта — решкой может упасть либо первая, либо вторая, либо третья монета, поэтому вероятность такого исхода равна 3 к 8.

А что произойдет, если мы подбросим четыре монеты, или пять, или семь, или девяносто?

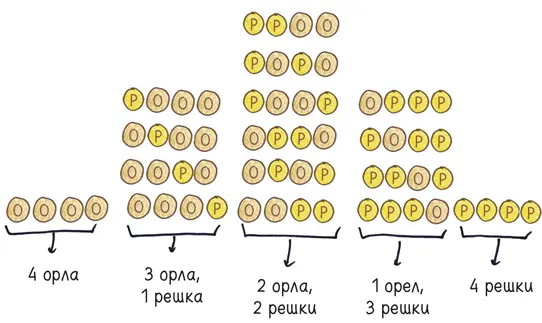
В данном случае мы исследуем семейство вероятностных моделей, известных под названием биномиальное распределение . Ваше единичное событие с двумя равновероятными исходами (орел или решка, победа или поражение, ноль или единица) происходит несколько раз. Это и есть биномиальность. И тогда, изучая эту ветвь математического генеалогического древа, мы наблюдаем две четких тенденции.

Первая: чем больше монет, тем сильнее расцветает сложность. Добавим одну монету, и количество потенциальных исходов увеличится вдвое, от 2 до 4, до 8, до 16. Подбрасывая десять монет, мы рассчитываем на чуть более чем тысячу различных исходов.

Подбросьте 50 монет, и количество исходов возрастет до 2 50, то есть больше квадриллиона. Эта тенденция агрессивного роста известна под названием комбинаторный взрыв . Линейный рост количества объектов ведет к экспоненциальному росту количества их комбинаций. Горсть монет, при всей своей кажущейся простоте, порождает непостижимое разнообразие.

Вторая тенденция обратная: даже если число вариантов быстро возрастает, доля необычных исходов сильно сокращается. Удостоверьтесь в этом на примере с четырьмя монетами, приведенном выше: есть всего два необычных варианта (все орлы и все решки) против 14 обыкновенных. Чем больше монет мы подбрасываем, тем меньше число необычных вариантов и тем глубже мы увязаем в трясине с практически равным соотношением орлов и решек.

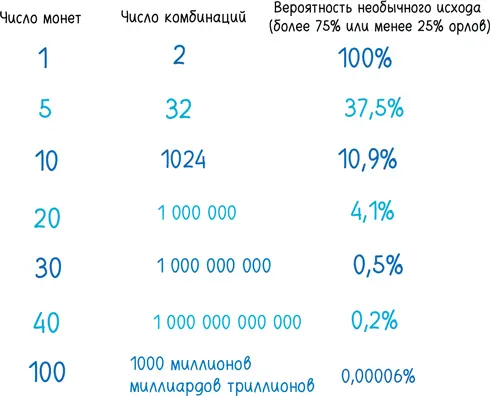
Причина проста. Обычные исходы обычны именно потому, что есть много вариантов получить их. В то же время необычные результаты необычны именно потому, что их редко можно получить [102] Та же логика лежит в основе концепции энтропии, тенденции Вселенной к беспорядку. Вообразите множество кирпичей. Есть крайне мало способов построить из них здание и много тоскливых, однообразных способов свалить их в кучу или разбить на осколки. Со временем случайные изменения накапливаются; есть почти нулевая вероятность, что кирпичи сами собой образуют здание; скорее всего, они всё больше будут рассыпаться. Таким образом, время предпочитает осколки, а не кирпичи. Точно так же у частиц пищевого красителя есть крайне мало способов собраться всем вместе с одной стороны стакана воды; все молекулы тогда как будто перекувыркнутся через голову. Но у этих частиц есть много-много способов более или менее равномерно распределиться внутри жидкости; каждое распределение будет похоже на уникальную комбинацию орлов и решек. Именно поэтому случайные процессы сумасбродно и неумолимо ведут к увеличению энтропии, равномерному смешению составных частей Вселенной. Космическое предпочтение беспорядка по сути своей комбинаторно. .