Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Предположим, мы подбрасываем 46 монет. Есть всего один вариант, когда все они выпадают орлом кверху.

Но допустим, нас интересуют исходы, когда единожды все-таки выпадает решка — возможно, это первая монета, или вторая, или третья, или четвертая, или пятая… и так далее вплоть до сорок шестой. Таким образом, есть 46 вариаций.

Сколько вариантов с двумя решками и 44 орлами? Еще больше. Решкой кверху могут выпасть первая и вторая монеты, или первая и третья, или первая и четвертая… или первая и последняя… или вторая и третья, или вторая и четвертая, или вторая и пятая… вплоть до второй и сорок шестой. В общей сложности есть более чем 1000 вариаций. Еще теплее! Наиболее вероятный исход — 23 орла и 23 решки — подразумевает восемь триллионов различных вариантов.

Я не экстрасенс, но если вы подбросите 46 монет, то я предвижу, что произойдет одно из двух:

1. От 16 до 30 монет выпадут орлом кверху [103] Вероятность этого варианта — около 96 %, поэтому в одном случае из 25 мое пророчество не сбудется. Однако если хотя бы 25 читателей действительно подбросят 46 монет, то аудитория научно-популярных книг по математике еще более упертая, чем я подозревал. .

2. Ваша последовательность будет исторической аномалией, уникальной в опыте всего человечества. Ни один подбрасыватель 46 монет еще не достиг ровно такого результата!

Отчего-то первый результат (серединный) затмевает второй (великолепный и уникальный). Для нас все монеты взаимозаменяемы, поэтому любая примерно сбалансированная последовательность орлов и решек будет казаться нам обычной и забудется, как снежинка во время метели.

Но представьте, что нас интересует структура этой снежинки. Представьте, что каждая последовательность орлов и решек для нас — особый поворот судьбы. Что, если нас тревожит не просто количество, но и конкретная последовательность орлов и решек?

Тогда любая из 70 триллионов возможных комбинаций станет для нас настолько исчезающе маловероятной, настолько вопиюще неожиданной, что ее появление покажется чудом. Она заворожит нас, словно звезда, сорвавшаяся с неба прямо к нам в руки. Эта последовательность 46 орлов и решек будет бесценна, как… ну, новорожденный малыш.

И это подводит нас к сложнейшему из двух вопросов главы: генетике.

Каждая клетка вашего тела содержит 23 пары хромосом. Представьте, что это поваренная книга в 23 томах, инструкция по изготовлению вашего организма, и у вас есть две версии каждого тома: мамина и папина.

Разумеется, у ваших родителей тоже есть по две копии: одна от вашей бабушки, другая от дедушки. Как они решили, какие именно хромосомы передать вам, своей драгоценной горошинке? Предположим, — и здесь я прибегаю к довольно театральному упрощению — они подбросили монету. Орел — вы получаете хромосому от дедушки. Решка — от бабушки.

Ваши родители повторили этот процесс по 23 раза, выбрали 23 тома, и в результате… ну, появились вы.

Исходя из этой модели у каждой семейной пары есть 2 46, или 70 триллионов, различных вариантов распорядиться своими хромосомами. В отличие от игры в орлянку, здесь детали имеют значение. Я унаследовал от матери густые волосы и тягу к чтению, а от отца — его походку и любовь к ясности. Если бы я унаследовал иную смесь их черт, например отцовские кудри и рост матери (или отсутствие того и другого), я бы стал другим человеком — своим собственным братом.

В наследовании генов орел и решка — не то же самое, что решка и орел.

Эта модель предсказывает различные степени сходства между братьями и сестрами, которые мы можем видеть. Одна крайность — всякий раз монета для младшего брата может выпасть так же, как для старшего. Несмотря на разницу в возрасте, такие братья, по сути дела, будут близнецами.

Другая крайность — ни одна монета не выпадает так, как в предыдущем случае. Тогда братья, словно в какой-нибудь жуткой книге Филиппа К. Дика, по отношению друг к другу будут генетическими чужаками, имеющими на биологическом уровне не больше общего, чем их родители {47} 47 Если совсем точно, одна хромосома, Y, у братьев обязательно будет общая, а у сестер — унаследованная от отца Х-хромосома. Но если взять брата и сестру, то при таком раскладе у них действительно не будет общих хромосом. — Прим. науч. ред. .

Разумеется, обе крайности маловероятны. Скорее всего, у братьев будет примерно половина общих хромосом из 46 — возможно, чуть больше, а возможно, чуть меньше. Согласно нашей биномиальной модели, львиная доля вариантов — от 18 до 28 общих хромосом.

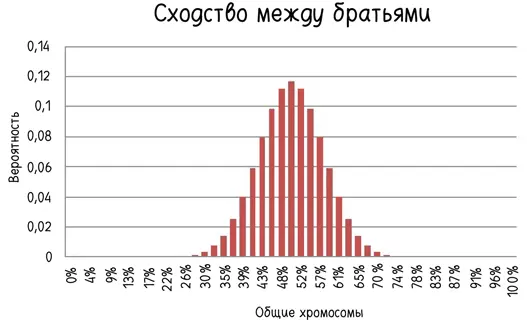
Данные примерно по 800 парам братьев и сестер, собранные Блейном Беттингером и опубликованные в его блоге «Генетический генеалог», показывают, что наш грубый прогноз был чертовски хорошим [104]:

Есть одно возражение. Я не упомянул настолько важный фактор, что не буду осуждать биологов, если прямо сейчас они яростно раздирают эту книгу на клочки. Это кроссинговер , или рекомбинация .

Я утверждал, что хромосомы передаются по наследству неповрежденными и нетронутыми. Это ложь, как и многие вещи, которые я говорил на уроках биологии. Прежде чем происходит выбор каждой версии хромосомы, две хромосомы склеиваются, например обмениваются средней третью. Таким образом, данная хромосома может преимущественно быть дедушкиной, но в ней будет несколько рецептов из бабушкиной поваренной книги.

Кроссинговер происходит примерно дважды с каждой хромосомой [105]. Таким образом, для повышения точности нашей модели мы можем утроить количество монет (потому что два кроссинговера расщепляют хромосому на три части).

Как это влияет на потенциальное количество детей, отличающихся друг от друга? Вспомните: линейный рост количества объектов приводит к экспоненциальному росту числа их комбинаций. Поэтому разнообразие потомков увеличится гораздо больше, чем в три раза. Точнее, от 2 46(около 70 триллионов) до 2 138(ошеломляющие 350 дуодециллионов {48} ).

Короче говоря, я утверждаю, что у новорожденного младенца много общего с горстью рассыпанных центов. Это не означает, что вы должны присвоить вашему ребенку цену $0,46. Наоборот, уронив на пол 46 центов, вы должны восхищаться, словно родился новый человек.