Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Я видел эти эскизы 4 июня 2017 года в прекрасном бельгийском музее Магритта. Советую посетить его, если вы окажетесь в Бельгии и захотите приправить сюрреализмом вашу картошку фри.

Это общепринятые финансовые термины, которые мне сообщила Джессика Джефферс. Я должен принести ей благодарность за помощь при работе над этой главой. Я шучу всего на 37 %, когда говорю, что Джесс — моя кандидатура на пост председателя Совета управляющих Федеральной резервной системы США.

Еще один важный источник этой главы (в особенности дискуссии о гауссовой копуле): Felix Salmon, «Recipe for Disaster: The Formula That Killed Wall Street». Wired , February 23, 2009, https://www.wired.com/2009/02/wp-quant/.

А также критическая доза сумасшествия (complete damn stupidity).

См. другой важный источник этой главы: Keith Hennessey, Douglas Holtz-Eakin and Bill Thomas, «Dissenting Statement», Financial Crisis Inquiry Commission, January 2011, https://fcic-static.law.stanford.edu/cdn_media/fcic-reports/fcic_final_report_hennessey_holtz-eakin_thomas_dissent.pdf.

James Surowiecki , The Wisdom of Crowds: Why the Many Are Smarter than the Few and How Collective Wisdom Shapes Business, Economies, Societies, and Nations (New York: Anchor Books, 2004). [ Шуровьески Дж. Мудрость толпы. Почему вместе мы умнее, чем поодиночке, и как коллективный разум влияет на бизнес, экономику, общество и государство. — М.: МИФ, 2014.]

Оррелл и Уилмотт.

Канеман Д. Думай медленно… Решай быстро. — М.: АСТ, 2013.

Благодарю Ричарда Бриджеса за (1) его помощь в подготовке этой главы и (2) за его платонизм, прагматизм, талант учителя, блестящий ум и доказательство того, что все эти качества могут уживаться в одном человеке.

Все данные из «Википедии». Ради вас, дорогой читатель, я использую самые надежные источники.

Loyd Grossman’s. Еще у них есть тикка-масала в банках.

Моим студентам всегда кажется странным и слишком запутанным возводить разницы в квадрат, складывать и потом извлекать квадратный корень. Почему бы просто не усреднить разности? То, что получится, называется «среднее абсолютное отклонение». Смысл его примерно тот же, что у среднеквадратичного отклонения, но ему не хватает важных теоретических свойств. Для статистических моделей важно, что легко вычислять дисперсии от сумм и произведений случайных величин.

Окей, пристегнитесь! Пора заняться кое-чем буйническим — это мое слово-гибрид от «буйный» и «технический». Для начала постройте диаграмму разброса данных, скажем рост (координата по горизонтали) и вес (по вертикали). Обозначьте каждого человека точкой.

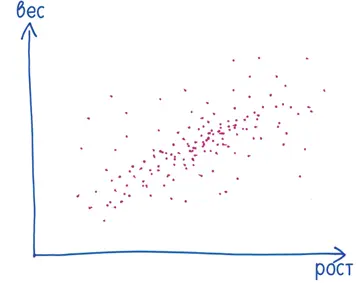
Теперь найдите средний рост и средний вес в этой популяции.

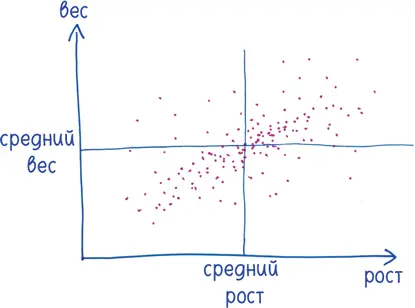
Затем возьмите отдельного человека. Насколько его вес и рост отличаются от средних значений? Если его вес/рост больше средних величин, засчитайте разницу как положительную, если меньше — как отрицательную.

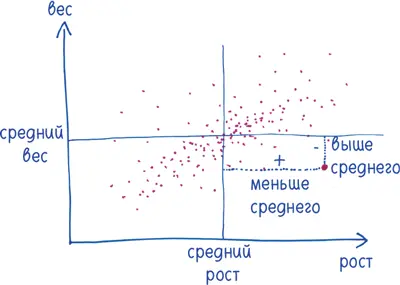
Затем — и это решающий шаг — перемножьте эти два значения. Если человек выше и тяжелее среднего, итог будет положительным. То же самое, если он ниже и легче среднего (потому что минус на минус дает плюс). Но если только одна из величин меньше среднего, результат будет отрицательным (потому что минус на плюс дает минус).

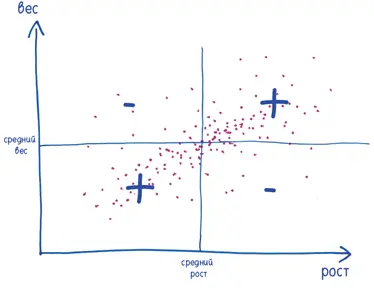
Проделайте эти вычисления для каждой точки, а затем найдите среднее арифметическое всех произведений. Эта величина называется ковариацией (кузина нашей знакомой дисперсии).

Вы почти у финиша! На завершающем этапе поделите это число, чтобы окончательный результат лежал между –1 и 1. (Поделить на что? Ну, подумайте о недостатке ковариации: если рост и вес людей весьма разнообразны, то отклонением от среднего, как правило, будет большее число. Другими словами, ковариация будет больше для неустойчивых величин и меньше для стабильных, вне зависимости от взаимосвязи между ними. Каким образом решить эту проблему? Просто поделите ковариацию на произведение среднеквадратичных отклонений — вы получите корреляцию.)

Уф! Теперь легкий этап: интерпретируем результаты.

Положительная корреляция (например, 0,8) подразумевает, что люди ростом выше среднего, как правило, еще и больше весят. Отрицательная корреляция (например, –0,8) подразумевает обратное: преобладают высокие худые люди или низкорослые толстяки. И наконец, корреляция, близкая к нулю, означает, что никакой значимой взаимосвязи нет. (На самом деле связь может быть, просто более сложная. — Прим. науч. ред. )

Цит. по книге: «Henry Chadwick», National Baseball Hall of Fame , http://baseballhall.org/hof/chadwick-henry. «Каждое движение, — сказал он о бейсболе, — стремительно, словно полет морской птицы». Мой друг Бен Миллер по этому поводу задался вопросом: африканской ласточки или европейской? (Цитата из знаменитого комедийного фильма «Монти Пайтон и Священный Грааль»: «Какова скорость полета порожней ласточки? — Какую ласточку вы имеете в виду — африканскую или европейскую?» — Прим. пер. ) (Ласточка — не морская птица. — Прим. науч. ред. )

Этот рекорд принадлежит отбивающему Брайану Лара из команды West Indies. В 2004 году во время матча с Англией он набрал ровно 400 пробежек без единого аута. Я рад странной статистической перекличке с названием этой главы.

Цит. по книге: Michael Lewis, Moneyball: The Art of Winning an Unfair Game (New York: W. W. Norton, 2003), 70. Никто не удивится, если я признаюсь, что эта глава в неоплатном долгу перед книгой «Манибол», и, если вы готовы вытерпеть историю бейсбольной статистики (дело десятое, интересна она вам или нет), вы получите удовольствие от этой книги.

Я взял для примера сезон английской Премьер-лиги, состоящий из 38 игр. Каждая игра длится 90 минут, накинем еще по 10 минут добавленного времени и получим в общей сложности 3800 минут. Двенадцать точек сбора данных в минуту (т. е. каждые 5 секунд) дадут 45 600 точек — все равно меньше, чем 48 000 в бейсболе, но довольно близко.

Ernest Hemingway, The Old Man and the Sea, Life , September 1, 1952. Над заглавием значилось: «Редакция журнала Life с гордостью представляет вниманию читателей новую великую книгу великого американского писателя, публикуемую впервые и в полном объеме».

Branch Rickey, «Goodby to Some Old Baseball Ideas», Life , August 2, 1954. Подзаголовок гласил: «Знаток игры приоткрывает формулу, которая с помощью статистики развенчивает лелеемые мифы и показывает, что побеждает на самом деле».