Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

• setup — задание системы линейных уравнений;

• standardize — приведение заданной системы уравнений или неравенств к стандартной форме неравенств типа «меньше или равно».

Главными из этих функций являются maximize и minimize, оптимизирующие задачу симплекс-методом. Они записываются в следующих формах:

maximize(f, С)

minimize(f, С)

minimize(f , С, vartype)

maximize(f , C, vartype)

maximize(f , C, vartype, 'NewC', 'transform')

minimize(f , C, vartype, 'NewC', 'transform')

Здесь f — линейное выражение, С — множество или список условий, vartype — необязательно задаваемый тип переменных NONNEGATIVE или UNRESTRICTED, NewC и transform — имена переменных, которым присваиваются соответственно оптимальное описание и переменные преобразования. Ниже даны примеры применения этих функций (файл simplex):

> restart:with(simplex):

Warning, the protected names maximize and minimize have been redefined and unprotected

> minimize(x+y, {4*x+3*y <= 5, 3*x+4*y <= 4}, NONNEGATIVE);

> minimize(x-y, {4*x+2*y <= 10, 3*x+4*y <= 16}, NONNEGATIVE, 'NC', 'vt');

> NC;vt;

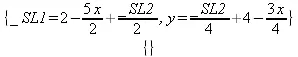
> maximize(x+y, {4*x+2*y <= 10, 3*x+4*y <= 16}, NONNEGATIVE);

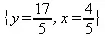
> maximize(x+y, {3*x+2*y <= 5, 2*x+4*y <=4});

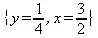
> z := 2*x1 - x2 + 3*x3;

> cnts1 := [x2+2*x3 <= 1, 2*x1-4*x2+6*x3 <= 3, -x1+3*x2+4*x3 <= 12];

> sol1 := maximize(z,cnts1,NONNEGATIVE);

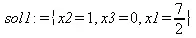
При использовании функций minimize и maximize надо не забывать, что это переопределенные функции — аналогичные по названию функции есть в ядре и они реализуют иные методы вычислений. Для возврата к исходному определению функций надо выполнить команду restart.

Функция basis(C) возвращает базис для системы линейных уравнений С. Например:

> basis([х = 2*z+w, z = 2*y-w]);

Функция convexhull(ps) возвращает выпуклую оболочку множества точек ps. Например:

> convexhull({[0,0], [1,1], [2,-1], [1,1/3],[1,1/2]));

Для определения констант для системы линейных уравнений или неравенств служит функция cterm(C):

> cterm([2*х+y<=6,7*y-z-3=4]);

Функция define zero(C) возвращает ближайшее ненулевое значение, зависящее от установки переменной Digits:

> define_zero();

> Digits:=40;

> define_zero();

> define_zero(1*10^(-10));

Функция display(C) имеет еще и форму display(C,[x, у, z]). Она задает вывод линейных уравнений и неравенств в матричной форме:

> display({2*x+5*y-z<= 0, 2*w-4*y-z<=2});

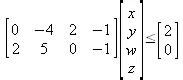
Функция dual(f, С, у) имеет следующие параметры: f — линейное выражение, С — множество неравенств и у — имя. Эта функция возвращает сопряженное с f выражение:

> dual(х-y,{2*х+3*y<=5,3*х+6*y<=15}, z);

Функция feasible может быть задана в трех формах:

feasible(С)

feasible(С,vartype)

feasible(С,vartype,'NewC','Transform')

Здесь параметр vartype может иметь значения NONNEGATIVE или UNRESTRICTED. Эта функция определяет систему как осуществимую или нет:

> feasible({2*х+3*y<=5, 3*х+6*y<=15), NONNEGATIVE);

> feasible({2*х+3*y<=5, 3*х+6*y<=-15}, NONNEGATIVE);

Если функция возвращает логическое значение true, то заданная система осуществима, а если false — неосуществима, то есть ни при каких значениях переменных не способна удовлетворить записанным неравенствам и равенствам.

Функция pivot(C, х, eqn) конструирует новую систему с заданным главным элементом:

> pivot({_SL1=5-4*x-3*y,_SL2=4-3*x-4*y),х,[_SL1=5-4*x-3*y]);

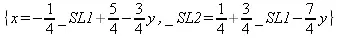
Функция pivoteqn(C, var) возвращает подсистему для заданного диагонального элемента С:

> pivoteqn((_SL1 = 5-3*х-2*y, _SL2 = 4-2*х-2*y}, х);

Функция pivotvar(f, List) или pivotvar(f) возвращает список переменных, имеющих положительные коэффициенты в выражении для целевой функции:

> pivotvar(x1-2*x2+3*x3-x4);

> pivotvar(x1+2*х3-3*х4, [x4,x3,x1]);

Функция ratio(C, х) возвращает список отношений, задающих наиболее жесткие ограничения:

> ratio([SL1=10-3*x-2*y, SL2=8-2*x-4*y], x);

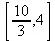
Функция setup может иметь три формы:

setup(С)

setup(С, NONNEGATIVE)

setup(С, NONNEGATIVE, 't')

Она обеспечивает конструирование множества уравнений с переменными в левой части:

> setup({2*х+3*y<=5,3*х+5*y=15));

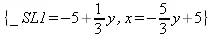
Последняя функция — standartize(C) — конвертирует список уравнений (неравенств) в неравенства типа «меньше или равно»:

> standardize({2*х+3*у<=5,3*х+5*у=15});

В систему Maple 9.5 был добавлен новый пакет оптимизации Optimization, основанный на новейших существенно улучшенных алгоритмах оптимизации. С его помощью можно решать не только задачи линейного, но и квадратичного и нелинейного программирований с повышенной степенью визуализации.

Пакет оптимизации Optimization вызывается как обычно:

> with(Optimization);

Warning, the name changecoords has been redefined

Для получения справки по пакету надо исполнить команду:

> help(Optimization);

Пакет использует при вычислениях алгоритмы группы NAG, которые считаются наиболее эффективными при реализации численных методов вычислений, в частности реализующих алгоритмы оптимизации. Пакет вводит 8 функций. Две из них это переопределенные функции вычисления максимума Maximize и минимума Minimize. Кроме того, пакет имеет 4 решателя уравнений с заданными ограничениями, реализующих следующие методы: