Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Возможна и матричная форма функции:

NLPSolve(n, р, nc, nlc, lc, bd, opts)

NLPSolve(n, р, lc, bd, opts)

Примеры на ее применение можно найти в справке по функции NLPSolve.

Для импорта данных из файлов служит функция:

ImportMPS(filename [, maxm, maxn, lowbnd, upbnd, opts])

В ней используются следующие параметры:

• filename — имя файла для MPS(X) в виде строки;

• maxm — максимальное число линейных ограничений;

• maxn — максимальное число переменных;

• lowbnd — значение нижней границы для переменных;

• upbnd — значение верхней границы для переменных;

• opts — выражения в виде опций, записываемых в форме option=value, где option один из объектов rhsname, rangename или boundsname, заданный для Import MPS команд.

С деталями применения этой функции можно ознакомиться по справке по ней.

Наконец в Maple 9.5 появились средства для полноценной нелинейной регрессии (реализации метод наименьших квадратов для произвольных приближающих зависимостей). Для этого служит функция:

LSSolve(obj, constr, bd, opts)

LSSolve(opfobj, ineqcon, eqcon, opfbd, opts)

Большинство ее параметров уже описывалось. Исключением является параметр opfobj — список процедур для остатков (разностей) метода наименьших квадратов. Пример применения этой функции для приближения облака заданных точек data нелинейной зависимостью с именем р дан на рис. 6.6.

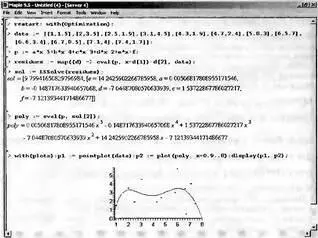
Рис. 6.6. Пример нелинейной регрессии с помощью функции LSSolve

Функция Interactive служит для организации интерактивной оптимизации в Maplet-окне. Эта функция может задаваться в виде:

Interactive()

Interactive(obj, constr)

В первом случае открывается «пустое» Maplet-окно, а во втором окно с введенной целевой функцией obj и ограничивающими условиями constr. Вид окна с примером квадратичной оптимизации представлен на рис. 6.7.

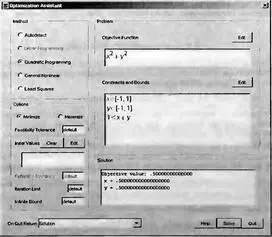
Рис. 6.7. Пример квадратичной оптимизации в Maplet-окне

В левом верхнем углу окна имеется список классов задач оптимизации. Справа расположены панели для ввода оптимизируемого выражения и ограничивающих условий. Кнопки Edit позволяют вызывать простые окна для редактирования их, а кнопка Solve запускает вычисления, результат которых появляется в окошке Solution. Остальные элементы интерфейса Maplet-окна в особых пояснениях не нуждаются.

Maple 10 позволяет решать задачи нелинейного программирования с ограничениями с помощью функции NPSolve из пакета оптимизации Optimization. Наглядный пример из самоучителя по Maple 10 представлен на рис. 6.8.

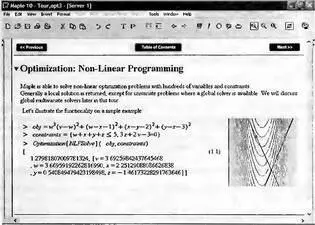
Рис. 6.8. Пример нелинейного программирования с ограничениями

Целевая функция задана значением переменной obj, а ограничивающие условия заданы переменной constraints. Решение очевидно и иллюстрируется контурным графиком функции и линиями ограничения.

Большим подспорьем в решении задач нелинейной регрессии стала реализация в Maple 9.5/10 нелинейного метода наименьших квадратов. Для Maple 9.5 эта реализация уже была описана. Рис. 6.9 иллюстрирует применение функции LSSolve для выполнения нелинейной регрессии общего вида. Этот пример также взят из самоучителя по Maple 10.

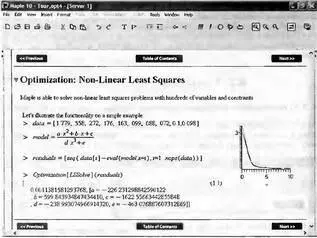
Рис. 6.9 Пример нелинейной регрессии в Maple

Данные data представляют собой ординаты зависимости y(i), где i задается целыми числами, начиная от 1 и до значения, равного числу чисел в векторе данных. Исходная функция задана переменной model. Возвращается значение погрешности и вычисленные параметры регрессионной зависимости. Расчет хорошо иллюстрируется графиком этой зависимости и исходными точками.

Большинство методов оптимизации способно отыскивать локальные экстремумы. Например, это позволяет функция NLPSolve из встроенного пакета оптимизации. Меняя точку начального выбора (инициализации) можно найти и глобальный экстремум для простых функций.

Но в Maple 10 есть возможность поиска глобального экстремума с помощью новой функции Global Solve пакета глобальной оптимизации, который можно найти в Интернете на сайте разработчика Maple 10. Пример этого для многоэкстремальной функции двух переменных представлен на рис. 6.10.

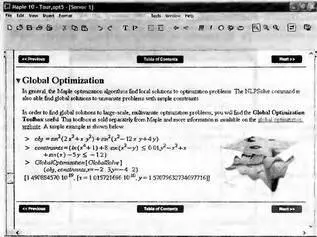
Рис. 6.10. Пример глобальной оптимизации многоэкстремальной функции двух переменных

Подлежащая глобальной оптимизации функция представлена значением переменной obj. Ее многоэкстремальный характер обусловлен синусоидальными компонентами. Ограничения заданы переменной constraints.

Для наглядного решения задач оптимизации можно применить маплет-ассистент оптимизации системы Maple 10. Ограничимся примером оптимизации многоэкстремальной функции одной переменной без ограничений — рис. 6.11. Такой вид окно имеет после ввода оптимизируемой функции с помощью кнопки Edit в области Objective Function. Выбор метода и прочие установки осуществлены по умолчанию (за исключением задания поиска максимума опцией Maximize).

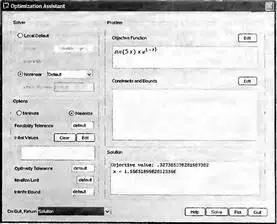
Рис. 6.11. Окно ассистента оптимизации с заданной функцией

Чтобы проверить, что же нашел ассистент оптимизации, желательно построить график функции. Для этого достаточно активизировать кнопку Plot в окне рис. 6.11. Будет построен график в области оптимизации. Расширив область графика до значений x от 0 до 6 получим график, представленный на рис. 6.12. Нетрудно заметить, что найден глобальный максимум в точке, отмеченной кружком.

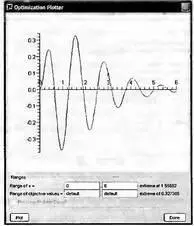
Рис. 6.12. График функции с помеченной точкой глобального максимума