Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Возможность выбора и решения с полсотни классических дифференциальных уравнений различного типа дает системе Maple 9.5 преимущества, которые по достоинству оценят пользователи, заинтересованные в знакомстве с такими уравнениями и в их использовании.

В Maple 9.5 средства решения дифференциальных уравнений подверглись значительной переработке. Введены новые методы решения для дифференциальных уравнений Абеля, Риккати и Матье, новые методы инициализации и решения уравнений с кусочными функциями, улучшены алгоритмы решения численными методами. Детальное описание этих новинок можно найти в справке по разделу What's New…. Это относится и к версии Maple 10.

Maple позволяет решать одиночные дифференциальные уравнения и системы дифференциальных уравнений как аналитически, так и в численном виде. Разработчиками системы объявлено о существенном расширении средств решения дифференциальных уравнений и о повышении их надежности в смысле нахождения решений для большинства классов дифференциальных уравнений.

Для решения системы простых дифференциальных уравнений ( задача Коши) используется функция dsolve в разных формах записи:

dsolve(ODE)

dsolve(ODE, y(x), extra_args)

dsolve({ODE, ICs}, y(x), extra_args)

dsolve({sysODE, ICs}, {funcs}, extra_args)

Здесь ODE — одно обыкновенное дифференциальное уравнение или система из дифференциальных уравнений первого порядка с указанием начальных условий, у(х) —функция одной переменной, Ics — выражение, задающее начальные условия, {sysODE} —множество дифференциальных уравнений, {funcs} — множество неопределенных функций, extra_argument —опция, задающая тип решения.

Параметр extra_argument задает класс решаемых уравнений. Отметим основные значения этого параметра:

• exact — аналитическое решение (принято по умолчанию);

• explicit — решение в явном виде;

• system — решение системы дифференциальных уравнений;

• ICs — решение системы дифференциальных уравнений с заданными начальными условиями;

• formal series — решение в форме степенного многочлена;

• integral transform — решение на основе интегральных преобразований Лапласа, Фурье и др.;

• series — решение в виде ряда с порядком, указываемым значением переменной Order;

• numeric — решение в численном виде.

Возможны и другие опции, подробное описание которых выходит за рамки данной книги. Его можно найти в справке по этой функции, вызываемой командой ?dsolve.

Для решения задачи Коши в параметры dsolve надо включать начальные условия, а при решении краевых задач — краевые условия. Если Maple способна найти решение при числе начальных или краевых условий меньше порядка системы, то в решении будут появляться неопределенные константы вида _С1, _С2 и т.д. Они же могут быть при аналитическом решении системы, когда начальные условия не заданы. Если решение найдено в неявном виде, то в нем появится параметр _Т. По умолчанию функция dsolve автоматически выбирает наиболее подходящий метод решения дифференциальных уравнений. Однако в параметрах функции dsolve в квадратных скобках можно указать предпочтительный метод решения дифференциальных уравнений. Допустимы следующие методы:

> `dsolve/methods`[1];

Более полную информацию о каждом методе можно получить, используя команду ?dsolve,method и указав в ней конкретный метод. Например, команда ?dsolve,linear вызовет появление страницы справочной системы с подробным описанием линейного метода решения дифференциальных уравнений.

Решение дифференциальных уравнений может сопровождаться различными комментариями. Команда

infolevel[dsolve] := n:

где n — целое число от 0 до 5 управляет уровнями детальности вывода. По умолчанию задано n = 0. Значение n = 5 дает максимально детальный вывод.

Производные при записи дифференциальных уравнений могут задаваться функцией diff или оператором дифференцирования D. Выражение sysODE должно иметь структуру множества и содержать помимо самой системы уравнений их начальные условия.

Читателю, всерьез интересующемуся проблематикой решения линейных дифференциальных уравнений, стоит внимательно просмотреть разделы справки по ним и ознакомиться с демонстрационным файлом linearoade.mws, содержащим примеры решения таких уравнений в закрытой форме.

Отвлекшись от физики, приведем несколько примеров на составление и решение дифференциальных уравнений первого порядка в аналитическом виде (файл dea):

> dsolve(diff(y(х),х)-а*х=0, y(х));

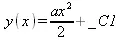
> dsolve(diff(y(х),х)-y(х)=ехр(-х), y(х));

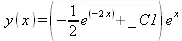
> dsolve(diff(y(х),х)-y(х)=sin(х)*х, y(х));

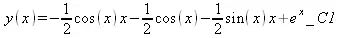
> infolevel[dsolve] := 3:

> dsolve(diff(y(x),x)-y(x)=sin(x)*x, y(x));

Methods for first order ODEs:

Trying classification methods —

trying a quadrature

trying 1st order linear

<- 1st order linear successful

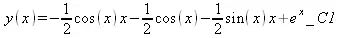
Обратив внимание на вывод в последнем примере. Он дан при уровне вывода n=3

Следующие примеры иллюстрируют возможность решения одного и того же дифференциального уравнения ode_L разными методами:

> restart: ode_L := sin(x)*diff(y(x),x)-cos(x)*y(x)=0;

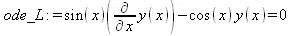
> dsolve(ode_L, [linear], useInt);

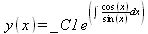
> value(%);

> dsolve(od_L, [separable], useInt);

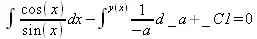
> value(%);

> mu := intfactor(ode_L);

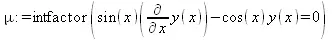
> dsolve(mu*ode_L, [exact], useInt);

Разумеется, приведенными примерами далеко не исчерпываются возможности аналитического решения дифференциальных уравнений.