Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Из приведенных выше примеров видно, что для задания производной используется ранее рассмотренная функция diff. С помощью символа $ в ней можно задать производную более высокого порядка.

В соответствии со вторым законом Ньютона многие физические явления, связанные с движением объектов, описываются дифференциальными уравнениями второго порядка. Ниже дан пример задания и решения такого уравнения (файл

dem), описывающего движение тела, брошенного вверх на высоте h 0со скоростью v 0при ускорении свободного падения g:

> restart; eq2:=diff(h(t),t$2) = -g;

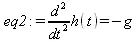
> dsolve({eq2,h(0)=h[0], D(h)(0)=v[0]},h(t));assign(s2);

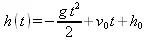
Итак, получено общее уравнение для временной зависимости высоты тела h(t). Разумеется, ее можно конкретизировать, например, для случая, когда g=9,8, h 0=10 и v 0=100:

> g:=9.8:

> s2:=dsolve({eq2,h(0)=10,D(h)(0)=100},h(t));assign(s2);

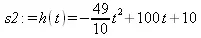
> plot(h(t),t=0..20,color=black);

Зависимость высоты тела от времени h(t) представлена на рис. 7.5. Нетрудно заметить, что высота полета тела вначале растет и достигнув максимума начинает снижаться. Оговоримся, что сопротивление воздуха в данном примере не учитывается, что позволяет считать задачу линейной. Полученное с помощью Maple 9.5 для этого случая решение совпадает с полученным вручную в примере, описанном в разделе 7.1.3.

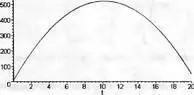
Рис. 7.5. Зависимость высоты полета тела от времени h(t)

Еще одним классическим применением дифференциальных уравнений второго порядка является решение уравнение идеального гармонического осциллятора (файл deio):

> restart:eq3:=diff(y(t),t$2)=-omega^2*y(t);

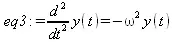
> dsolve(eq3,y(t));

> s:=dsolve({eq3,y(0)=-1,D(y)(0)=1}, y(t));

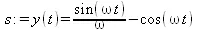
> assign(s);omega:=2;

> plot(y(t),t=0..20,color=black);

График решения этого уравнения (рис. 7.6) представляет хорошо известную синусоидальную функцию. Интересно, что амплитуда колебаний в общем случае отлична от 1 и зависит от значения у(0) — при у(0)=0 она равна 1 (в нашем случае синусоида начинается со значение у(0)=-1). Подобным осциллятором может быть LC-контур или механический маятник без потерь.

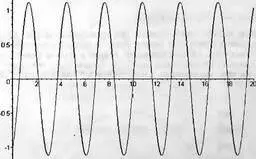
Рис. 7.6. Решение дифференциального уравнения идеального осциллятора

Ниже представлено решение еще двух дифференциальных уравнений второго порядка в аналитическом виде (de2a):

> restart: dsolve(diff(y(x),x$2)-diff(y(x),x)=sin(x),y(x));

> de:=m*diff(y(x),x$2)-k*diff(y(x),x);

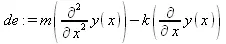
> yx0:=y(0)=0,y(1)=1;

> dsolve({de,yx0},y(x));

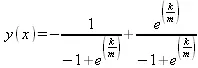
Ряд примеров на применение дифференциальных уравнений второго порядка при решении практических математических и физических задач вы найдете в главе 11.

Функция dsolve позволяет также решать системы дифференциальных уравнений. Для этого она записывается в виде

dsolve(ODE_sys, optional_1, optional_2,...)

Здесь ODE_sys — список дифференциальных уравнений, образующих систему, остальные параметры опциональные и задаются по мере необходимости. Они могут задавать начальные условия, явно представлять искомые зависимости, выбирать метод решения и т.д. Детали задания опциональных параметров можно найти в справке.

На рис. 7.7 представлено решение системы из двух дифференциальных уравнений различными методами — в явном виде, в виде разложения в ряд и с использованием преобразования Лапласа. Здесь следует отметить, что решение в виде ряда является приближенным. Поэтому полученные в данном случае аналитические выражения отличаются от явного решения и решения с применением преобразования Лапласа.

Рис. 7.7. Решение системы из двух дифференциальных уравнений различными методами

Следует отметить, что, несмотря на обширные возможности Maple в области аналитического решения дифференциальных уравнений, оно возможно далеко не всегда. Поэтому, если не удается получить такое решение, полезно попытаться найти решение в численном виде. Практически полезные примеры решения дифференциальных уравнений, в том числе с постоянными граничными условиями, вы найдете в Главе 11.

В качестве еще одного примера решении системы из двух дифференциальных уравнений рассмотрим модель Стритера-Фелпса, предложенную для описания динамики содержания растворенного в воде кислорода. Описание этой модели можно найти в [41]. Ниже представлено задание этой модели в виде системы из двух дифференциальных уравнений и их аналитическое решение (файл demp):

> sys := diff(x1(t),t) = K1*(C-x1(t))-K2*x2(t), diff(x2(t),t) = -K2*x2(t);

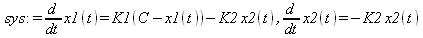
> dsol := dsolve({sys,x1(0) =a, x2(0)=b),{x1(t),x2(t)});

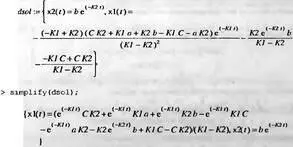
Здесь: x1(t) — концентрация в воде растворенного кислорода в момент времени t; x2(t) — концентрация биохимического потребления кислорода (БПК), С — концентрация насыщения воды кислородом, K1 — постоянная скорости аэрации, K2 — постоянная скорости уменьшения (БПК), a — начальное значение x1(t) и b — начальное значение х2(t) при t=0.

В данном случае получены два варианта аналитического решения — основное и упрощенное с помощью функции simplify. Читатель может самостоятельно построить графики зависимостей x1(t) и x2(t).