Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

Дифференциальные уравнения лежат в основе математического моделирования различных, в том числе физических, систем и устройств [1, 38, 46]. Решению таких уравнений посвящена эта глава. В ней рассмотрено как аналитическое, так и численное решение дифференциальных уравнений различного вида — линейных и нелинейных, классических и специальных, например, в частных производных и с учетом двухсторонних граничных условий. Описание сопровождается множеством наглядных примеров, реализованных в СКМ Maple 9.5/10.

Дифференциальные уравнения (ДУ) это уравнения, связывающие неизвестную функцию с какими либо ее производными и, возможно, с независимыми переменными. Если неизвестная функция зависит только от одной независимой переменной, то такое уравнение называется обыкновенным дифференциальным уравнением , а если от двух и более многих независимых переменных — дифференциальным уравнением в частных производных.

Простейшее дифференциальное уравнение первого порядка

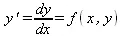(7.1)

в общем случае имеет множество решений в виде зависимостей y(х). Однако можно получить единственное решение, если задать начальные условия в виде начальных значений х 0и у 0= у(х 0). Это решение может быть аналитическим, конечно-разностным или численным.

В качестве примера аналитического решения дифференциального уравнения первого порядка (файл der) запишем дифференциальное уравнение радиоактивного распада атомов ( N — число атомов в момент времени t, g= 1/c):

> restart: deq:=diff(N(t),t)=-g*N(t);

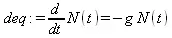
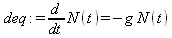
Используя функцию dsolve, которая более подробно будет описана чуть позже, получим его общее аналитическое решение:

> dsolve(deq, N(t));

В решении присутствует произвольная постоянная _С1. Но ее можно заметить на постоянную N(0)=N 0, означающую начальное число атомов в момент t=0:

> dsolve({deq,N(0)=No},N(t));

Если конкретно N 0= 100 и g= 4, то получим:

> No := 100; g:=3;

Хотя dsolve выдает решение N(t) в символьном виде, оно пока недоступно для построения графика этого решения или просто вычисления в любой точке. Однако, используя функции assign или subs можно сделать это решение доступным. Например, используем такую конструкцию:

> s: =dsolve({ deq, N(0) =-No}, N (t)); assign(s);

Теперь мы можем воспользоваться полученной зависимостью N(t) и построить граф и к ее:

> plot(N(t),t=0..3,color=black);

Этот график, который читатель может просмотреть сам, описывает хорошо известным апериодическим экспоненциальный закон уменьшения числа атомов вещества в ходе его радиоактивного распада. Подобные зависимости, кстати, характерны для напряжения на конденсаторе С при его разряде через резистор R, для тока в LA-цепи и для многих простых физических явлений, описывающихся дифференциальным уравнением первого порядка.

Еще одним классическим примером применения дифференциального уравнения первого порядка является давно известная и довольно грубая модель популяции Мальтуса. Не вдаваясь в хорошо известное описание этой модели, отметим, что она описывает численность особей или их биомассу x(t) в любой момент времени (для момента времени х(0)=N) Эта зависимость характеризуется коэффициентами рождаемости α и смертности β. При этом вводится их разность k=α-β.

Представим задание дифференциального уравнения динамики популяций по модели Мальтуса и его решение в аналитическом виде:

> restart:deq := diff(х(t),t) - k*x(t)=0;

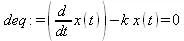
> dsol1 := dsolve({deq,x(0)=N});

Нетрудно заметить, что решение этого уравнения аналогично решению дифференциального уравнения радиоактивного распада и описывается также экспоненциальной функций. Однако, в зависимости от того, какой фактор (рождаемость или смертность) преобладает наблюдается либо экспоненциальный рост, либо экспоненциальный спад биомассы популяций.

Более правдоподобную модель популяций предложили Ферхюльст и Пирл. Эта модель учитывает (коэффициентом внутривидовую конкуренцию и позволяет учесть приближение популяций к некоторому состоянию равновесия. На рис. 7.1 представлено дифференциальное уравнение динамики популяций Ферхюльста-Пирла. Решения приведены в общем виде, а также для k=g= k/g= 1 и разных x(0)=1, 0.5 и 2.

Рис. 7.1. Моделирование популяций по модели Ферхюльста и Пирла

Поведение системы зависит от соотношения k/g и x(0)=N. При их равенстве количество биомассы популяции не меняется. При N>k/g биомасса экспоненциально уменьшается, приближаясь к значению k/g, а при N она экспоненциально возрастает, также приближаясь к k/g.

Встроенные в математические системы функции обычно решают систему из обыкновенных дифференциальных уравнений (ОДУ), представленную в форме Коши:

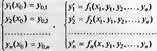
Здесь левая система задает начальные условия, а вторая представляет систему ОДУ.

Часто встречаются ДУ высокого (n-го) порядка:

где

Обозначив

и

Теперь решение этого уравнения можно свести к решению системы ОДУ: