Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

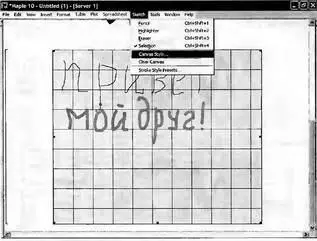
Рис. 8.86. Пример вставки наброска и рисования в нем

Те же самые средства имеются в контекстном меню правой клавиши мыши. Для редактирования набросков служит команда Canvas Style..., которая выводит окно редактирования, представленное на рис. 8.87. В окне можно задавать вывод вертикальным и горизонтальных линий сетки, устанавливать расстояние между ними (шаг) и изменять цвета объектов наброска — линий разметки и фона. Окно выбора цвета показано также на рис. 8.87.

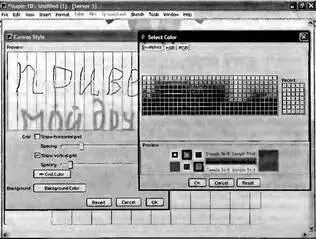
Рис. 8.87. Окно редактирования набросков (слева) и окно установки цвета (справа)

Команда Stroke Styles… открывает окно установки стиля карандаша и распылителя, показанное на рис. 8.88 с открытой вкладкой карандаша. Помимо заведомо определенных стилей можно задать свой собственный стиль и установить для него толщину линии и ее цвет. Аналогичные средства для распылителя есть на второй вкладке этого окна.

Рис. 8.88. Окно установки стилей карандаша и распылителя

Представленные выше графики записаны в файл newg_m10. Применение графических набросков разнообразит документы системы Maple 10

В представленных выше главах описан ряд пакетов расширения системы Maple, которые широко применяются в практике математических и научно-технических расчетов. Эти пакеты были рассмотрены достаточно подробно. В этой небольшой главе обзорно описаны пакеты расширения системы Maple, представляющие ограниченный интерес для большинства пользователей системы. Но они интересуют опытных пользователей — математиков и специалистов по программированию. Заинтересовавшийся ими читатель может дополнить сведения об этих пакетах просмотром справки и демонстрационных примеров в ней.

Пакет геометрических расчетов загружается командой

> with(geometry);

которая возвращает весьма внушительный список из более чем 100 функций. Ввиду его громоздкости список не приводится. Функции пакета имеют типовые для объектов двумерной графики имена и рассчитаны на выборочное использование (это, кстати, характерно для средств и других пакетов этой главы).

Этот пакет содержит средства расчета основных параметров ряда геометрических объектов. Для каждого объекта возможно задание различных исходных величин, так что пакет охватывает практически все виды классических геометрических расчетов на плоскости. Несомненно, этот пакет заинтересует всех, кто работает в области геометрии и смежных с нею областях.

Обратите внимание на то, что большинство функций этого пакета вовсе не рисуют на экране соответствующие фигуры, а лишь выполняют типовые геометрические расчеты. Разумеется, в дальнейшем, используя результаты этих расчетов, можно построить соответствующую фигуру с помощью графических функций.

Учитывал идентичность идеологии при работе с функциями этого пакета, большинство из которых имеет вполне прозрачные имена (правда, англоязычные), работу с пакетом поясним на примере одной из функций — circle. Она позволяет математически задать окружность и определить все ее геометрические параметры. Функция может иметь несколько форм записи. Например, в форме

circle(с, [А, В, С], n, 'centername'=m)

она определяет построение окружности, проходящей через три точки А, В и С. Необязательный параметр n — список с именами координатных осей. Параметр 'centername'=m задает имя центра.

В форме

circle(с, [А, В], n, 'centername'=m)

задается окружность, проходящая через две точки А и В, а в форме

circle(с, [A, rad], n, 'centername'=m)

задается окружность, проходящая через одну точку А с заданным (и произвольным) радиусом rad и центром с. Наконец, функция circle в форме

circle(с, eqn, n, 'centername'=m )

позволяет задать окружность по заданным уравнению eqn и центру с.

Проиллюстрируем применение функции circle на следующих примерах. Зададим характеристические переменные:

> _EnvHorizontalName := m: _EnvVerticalName := n:

Определим окружность с1, проходящую через три заданные точки А, В и С с указанными после их имен координатами и найдем координаты центра этой окружности:

> circle(c1,[point(А,0,0), point(В,2,0),point(С,1,2)], 'centername'=O1):

> center(c1), coordinates(center(c1));

Далее найдем радиус окружности

> radius(c1);

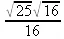
и уравнение окружности, заданное в аналитическом виде:

> Equation(c1);

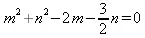
Наконец, с помощью функции detail получим детальное описание окружности:

> detail(c1);

Одно из важных достоинств пакета geometry — возможность наглядной визуализации различных геометрических понятий, например, графической иллюстрации доказательства теорем или геометрических преобразований на плоскости. Проиллюстрируем это на нескольких характерных примерах, заодно показывающих технику работы с рядом функций этого пакета.

Рис. 9.1 показывает построение из множества окружностей фигуры — кардиоиды. Вопреки обычному построению этой фигуры, используется алгоритм случайного (но удовлетворяющего требованиям построения данной фигуры) выбора положений центров и радиусов окружностей.

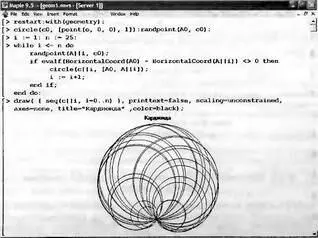
Рис. 9.1. Построение кардиоиды из окружностей

Рис. 9.2 дает графическую иллюстрацию к одной из теорем Фейербаха. Здесь эффектно используются средства выделения геометрических фигур цветом, что, увы, нельзя оценить по книжной чёрно-белой иллюстрации.

Рис. 9.2. Графическая иллюстрация к теореме Фейербаха