Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

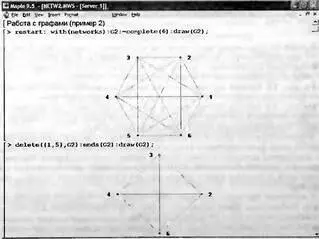
Рис. 9.9. Преобразование графа удалением части вершин

В третьем примере (рис. 9.10) граф формируется по частям — вначале задается пустой граф функцией new, а затем с помощью функций addvertex и addedge в него включаются вершины и ребра. Далее функция connect соединяет вершину a с вершиной с, делая граф замкнутым. Функция draw строит сформированный таким образом граф, а функции head и tail используются для выявления «голов» и «хвостов» графа.

Рис. 9.10. Формирование графа и определение его «голов» и «хвостов»

В четвертом примере, представленном на рис. 9.11, показано создание графа G2 (его изображение было приведено на рис. 9.9) с вычислением для этого графа максимального потока от вершины 1. Обратите внимание, что в параметрах функции flow, использованной для этого, заданы две переменные: eset — принимает значение множества с ребрами, по которым проходит максимальный поток, и comp — принимает значение множества, в котором содержатся вершины , по которым проходит максимальный поток. Значения этих переменных выведены в области вывода. В заключительной части этого примера показано применение функции shortpathtree, ищущей наиболее короткий путь от вершины 1 до других вершин.

Рис. 9.11. Пример вычисления максимального потока и наиболее коротких путей для заданного графа

Приведенный ниже еще один пример иллюстрирует работу функции show, выдающей таблицу с полной информацией о графе, созданном функцией complete:

> restart:with(networks):G2:=complete(4):

> show(G2);

Разумеется, приведенные примеры далеко не исчерпывают всех задач, которые можно решать с применением графов. Но они наглядно демонстрируют, что для большинства пользователей пакет networks превращает графы из окутанного ореолом таинственности модного средства в простой рабочий инструмент.

Этот пакет полезен математикам, часто использующим рекуррентные отношения и формулы. Он дополняет функцию rsolve основной библиотеки и содержит следующие функции:

> with(LREtools);

В пакете дифференциальных форм содержится следующий ряд функций:

> with(difforms);

Демонстрационные материалы по применению этого пакета входят в поставку Maple, так что заинтересованный читатель может их просмотреть.

Этот пакет впервые появился в реализации Maple V R5. Он дает средства для работы с тензорами и вычислениями, используемыми в общей теории относительности. В нем использован специальный тип данных tensor_type в виде таблиц с двумя полями: компонентов и характеристик индексов. Поле компонентов — массив с размерностью, эквивалентной рангу объекта. Поле характеристик индексов задается списком чисел 1 и -1. При этом 1 на i-й позиции означает, что соответствующий индекс контравариантный, а -1 — что он ковариантный.

Процедура tensor_type возвращает логическое значение true, если ее первый аргумент удовлетворяет свойствам тензора, и false, если он этому свойству не удовлетворяет.

Каждому тензору соответствуют еще две таблицы. Таблица коэффициентов вращения задает коэффициенты вращения Ньюмена-Пенроуза, которые вычисляются функцией tensor[npspin] и индексируются именами греческих букв alpha, beta, gamma, epsilon и т.д. Другая таблица (компонент кривизны) содержит компоненты кривизны Ньюмена-Пенроуза. Они представлены тремя полями: полем Phi в виде массива размерности (0..2,0..2) с компонентами Риччи, поле Psi с массивом размерности (0..4) с компонентами Вейля и поле R со скаляром Риччи.

Объявление

> with(tensor);

дает доступ к множеству функций пакета:

Christoffel1 — вычисление символов Кристоффеля первого рода;

Christoffel2 — вычисление символов Кристоффеля второго рода;

Einstein — возвращает тензор Эйнштейна;

display_alJGR — описывает ненулевые компоненты всех тензоров и параметров, вычисленных командой tensorsGR (общая теория относительности);

displayGR — описывает ненулевые компоненты конкретного тензора (общая теория относительности);

Jacobian — Якобиан преобразования координат;

Killing_eqns — вычисляет компоненты для уравнений Киллинга (имеет отношение к симметриям пространства);

LeviCivita — вычисляет ковариантные и контравариантные псевдотензоры Леви-Чивита;

Lie_diff — вычисляет производную Ли тензора по отношению к контравариантному векторному полю;

Ricci — тензор Риччи;

Ricciscalar — скаляр Риччи;

Riemann — тензор Римана;

RiemannF — тензор кривизны Римана в жесткой системе отсчета;

tensorsGR — вычисляет тензор кривизны в данной системе координат (общая теория относительности);

Weyl — тензор Вейля;

act — применяет операции к элементам тензора, таблицам вращений или кривизны;

antisymmetrize — антисимметризация тензора по любым индексам;

change_basis — преобразование системы координат;

commutator — коммутатор двух контравариантных векторных полей;

compare — сравнивает два тензора, таблицы вращений или кривизны;

conj — комплексное сопряжение;

connexF — вычисляет связующие коэффициенты для жесткой системы координат;

contact — свертка тензора по парам индексов;

convertNP — преобразует связующие коэффициенты или тензор Римана к формализму Ньюмена-Пенроуза;

cov_diff — ковариантное дифференцирование;

create — создает тензорный объект;