Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

d1metric — первая частная производная метрики;

d2metric — вторая частная производная метрики;

directional_diff — производная по направлению,

dual — осуществляет дуальную операцию над индексами тензора;

entermetric — обеспечивает ввод пользователем координатных переменных и ковариантных компонент метрического тензора;

exterior_diff — внешнее дифференцирование полностью антисимметричного ковариантного тензора;

exterior_prod — внешнее произведение двух ковариантных антисимметричных тензоров;

frame — задает систему координат, которая приводит метрические компоненты к диагональной сигнатурной матрице (с положительными или отрицательными единицами);

geodesic_eqns — уравнение Эйлера-Лагранжа для геодезических кривых;

get_char — возвращает признак (ковариантный/контравариантный) объекта;

getcompts — возвращает компоненты объекта;

get_rank — возвращает ранг объекта;

invars — инварианты тензора кривизны Римана (общая теория относительности);

invert — обращение тензора второго ранга;

lincom — линейная комбинация тензорных объектов;

lower — опускает индексы;

npcurve — компонента кривизны Ньюмена-Пенроуза в формализме Дебевера (общая теория относительности);

npspin — компонент вращения Ньюмена-Пенроуза в формализме Дебевера (общая теория относительности);

partial_diff — частная производная тензора;

permute_indices — перестановка индексов;

petrov — классификация Петрова тензора Вейля;

prod — внутреннее и внешнее тензорное произведения;

raise — поднятие индекса;

symmetrize — симметризация тензора по любым индексам;

transform — преобразование системы координат.

Пакет представляет несомненный интерес для физиков-теоретиков, работающих в области общей теории относительности и ее приложений. Для них (но не для большинства пользователей) отмеченные выше данные полезны и понятны.

Этот небольшой пакет служит для создания доменов — таблиц операций для вычислений. При его загрузке появляется сообщение о переопределениях объектов и список из всего лишь шести функций:

> restart;with(Domains);

-------------------- Domains version 1.0 -----------------------

Initially defined domains are Z and Q the integers and rationals

Abbreviations, e.g. DUP for DenseUnivariatePolynomial, also made

Warning, the protected names Array, Matrix and Vector have been

redefined and unprotected

Пакет допускает применение следующих конструкций:

Domains[domain]

Domains[evaldomains]

Domains[example]

Domains[coding]

Приведенный ниже пример поясняет создание и использование доменов Q (для рациональных данных) и Z (для целочисленных данных):

> Q[`+`] (1/2,2/5,3/8);

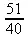
> Z[Gcd](660,130);

Следующая операция показывает, что домен Z является таблицей:

> type(Z,table);

А функция show позволяет вывести полный перечень всех операций, доступных для домена Z:

> show(Z,operations);

` Signatures for constructor Z`

` note: operations prefixed by — are not available`

` * : (Integers,Z) -> Z`

` * : (Z,Z*) -> Z`

` + : (Z,Z*) -> Z`

` - : Z -> Z`

` - : (Z,Z) -> Z`

` 0 : Z`

` 1 : Z`

` < : (Z,Z) -> Boolean`

` <= : (Z,Z) -> Boolean`

` <> : (Z,Z) -> Boolean`

` = : (Z,Z) -> Boolean`

` > : (Z,Z) -> Boolean`

` >= : (Z,Z) -> Boolean`

` Abs : Z -> Z`

` Characteristic : Integers`

` Coerce : Integers -> Z`

` Div : (Z,Z) -> Union(Z,FAIL)`

` EuclideanNorm : Z -> Integers`

` Factor : Z -> [Z, [ [Z,Integers]*]`

` Gcd : Z* -> Z`

` Gcdex : (Z,Z,Name) -> Z`

` Gcdex : (Z,Z,Name, Narre) -> Z`

` Input : Expression -> Union(Z,FAIL)`

` Inv : Z -> Union(Z,FAIL)`

` Lcm : Z* -> Z`

` Max : (Z,Z*) -> Z`

` Min : (Z,Z*) -> Z`

` Modp : (Z,Z) -> Z`

` Mods : (Z,Z) -> Z`

` ModularHomomorphism : () -> (Z -> Z,Z)`

` Normal : Z -> Z`

` Output : Z -> Expression`

` Powmod : (Z,Integers,Z) -> Z`

` Prime : Z -> Boolean`

` Quo : (Z,Z,Name) -> Z`

` Quo : (Z,Z) -> Z`

` Random : () -> Z`

` Relatively Prime : (Z,Z) -> Boolean`

` Rem : (Z,Z,Name) -> Z`

` Rem : (Z,Z) -> Z`

` Sign : Z -> UNION(1,-1,0)`

` SmallerEuclideanNorm : (Z,Z) -> Boolean`

` Sqrfree : Z -> [Z, [[Z,Integers]*]]`

` Type : Expression -> Boolean`

` Unit : Z -> Z`

` UnitNormal : Z -> [Z,Z,Z]`

` Zero : Z -> Boolean`

` ^ : (Z,Integers) -> Z`

Домены позволяют передавать в качестве параметра процедур набор функций в виде единого целого, что и объясняет название этих объектов. Предполагается, что это может привести к заметному сокращению кодов программ вычислений в будущих реализациях системы Maple. Пока же возможности доменов скорее выглядят как очередная экзотика, чем как реальное средство для оптимизации вычислений. Потребуется время, чтобы показать, что это не так.

Пакет Ore_algebra содержит набор функций алгебры линейных операторов, состав которого можно получить после обращения к пакету:

> with(Ore_algebra);

Этот пакет поддерживает решение задач в области алгебры линейных операторов. Примеры на его применения можно найти в справке и в файле Ore_algebra, имеющимся на Интернет-сайте корпорации MapleSoft.

В пакете genfunc, предназначенном для работы с производящими функциями содержатся функции, список которых выводит команда:

> with(genfunc);

Эти функции представляют специальный интерес для пользователей, работающих в области теории чисел и рациональных функций.

Этот пакет содержит довольно представительный набор функций для работы с конечными группами. Вывод списка функций обеспечивает команда:

> with(group);

Функции этого пакета представляют интерес для математиков, работающих в области конечных групп. Но вряд ли они будут полезны большинству пользователей. Тем не менее, наличие таких функций говорит о полноте функциональных возможностей системы Maple.