Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Рис. 77

В начале 1920 годов золотое сечение применял еще один художник – итальянский живописец Джино Северини (1883–1966). В своей работе Северини пытался примирить несколько противоречивые цели футуризма и кубизма. Футуризм отражал стремление группы итальянских мыслителей, работавших в области литературы, изобразительного искусства, театра, музыки и кинематографа, способствовать обновлению итальянской культуры. По словам самого Северини: «Мы решили сосредоточить внимание на предметах в движении, поскольку современный тип чувствительности особенно предрасположен к тому, чтобы ухватить идею скорости». Первый манифест художников-футуристов был подписан в 1910 году и всячески побуждал молодых итальянских художников «глубоко презирать всевозможную имитацию». Оставаясь футуристом, Северини обрел в кубизме «идею меры», которая соответствовала его честолюбивому стремлению «живописными средствами создать объект, столь же совершенный с точки зрения мастерства, что и великолепный буфет работы краснодеревщика». Такое стремление к геометрическому совершенству заставило Северини применять золотое сечение в подготовительных эскизах к нескольким работам (см. «Материнство», сейчас хранится в частной коллекции в Риме, рис. 78). Интересный пример роли золотого сечения в кубистическом искусстве – творчество русской художницы-кубистки Марии Воробьевой, известной как Маревна (1892–1984). В 1974 году Маревна написала книгу «Моя жизнь с художниками “Улья”», где очень увлекательно рассказывает о жизни и работе своих друзей – группы, куда входили художники Пикассо, Модильяни, Сутин, Ривера (от которого у Маревны родилась дочь) и другие – в Париже в двадцатые годы. Хотя Маревна не приводит никаких конкретных примеров, а ее исторические замечания зачастую неточны, из текста следует, что Пикассо, Ривера и Грис применяли золотое сечение как очередной, более сложный способ делить плоскость, предназначенный для знатоков и ценителей.

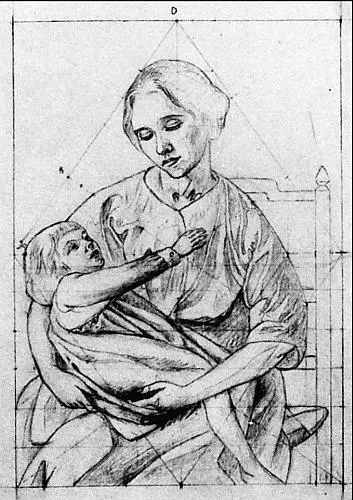
Рис. 78

В начале ХХ века золотым сечением очень интересовался и американский искусствовед Джей Хембридж (1867–1924). Хембридж выпустил целый ряд статей и книг, где определял два типа симметрии в классическом и современном искусстве. Первый он назвал статической симметрией, и такая симметрия основана на правильных фигурах наподобие квадрата и равностороннего треугольника и, по мнению исследователя, приводила к созданию безжизненных произведений искусства. В создании другой симметрии, которую он назвал динамической, главную роль играли золотое сечение и логарифмическая спираль. Главный тезис Хембриджа состоял в том, что применение динамической симметрии в композиции приводит к созданию живых и трогательных произведений искусства. Сегодня лишь немногие воспринимают его идеи всерьез.

Одним из самых ярых сторонников применения золотого сечения в искусстве и архитектуре был знаменитый швейцарско-французский архитектор и художник Ле Корбюзье (Шарль-Эдуар Жаннере-Гри, 1887–1965). Жаннере родился в Ла-Шо-Де-Фон в Швейцарии, где учился живописи и гравюре. Отец его работал эмальером в часовой мастерской, а мать была пианисткой и учительницей музыкой и, помимо более абстрактных занятий, всячески склоняла сына стать музыкантом-виртуозом… В 1905 году Жаннере стал изучать архитектуру и впоследствии стал одной из самых влиятельных фигур в современной архитектуре. Зимой 1916–1917 года Жаннере переехал в Париж и познакомился там с Амеде Озанфаном, который был вхож в высшее парижское общество художников и мыслителей. Благодаря Озанфану Жаннере познакомился с кубистами и невольно перенял их эстетические взгляды. В частности, Хуан Грис заразил его интересом к системам пропорций и их роли в эстетике. Осенью 1918 года Жаннере и Озанфан устроили совместную выставку в галерее Тома. Точнее, две картины Жаннере соседствовали с куда более многочисленными полотнами Озанфана. Озанфан и Жаннере назвали себя пуристами, а каталог своей выставки озаглавили « Après le Cubisme » – «После кубизма». Пуризм возрождает идеи Пьеро делла Франческа и платоновской эстетической теории: он утверждает, что «произведение искусства не должно быть случайным, исключительным, импрессионистским, неорганичным, протестным, картинным – напротив, оно должно быть обобщенным, статичным, выразительным за счет постоянства».

Псевдоним Ле Корбюзье (позаимствованный у предков с материнской стороны, чья фамилия была Лекорбезье) Жаннере взял лишь в 33 года, когда он уже пустил корни в Париже и был уверен в своем будущем. Судя по всему, он в целом хотел перечеркнуть мелкие неудачи прошлого и создать миф о том, что его архитектурный гений расцвел в одночасье. Поначалу Ле Корбюзье относился к применению золотого сечения в искусстве довольно-таки скептически и даже отрицательно – он предостерегал против того, чтобы «замещать здравый смысл мистицизмом при помощи золотого сечения». Более того, подробный анализ архитектурных проектов и «пуристских» работ Ле Корбюзье, который проделал Роджер Герц-Фишлер, показывает, что до 1927 года Ле Корбюзье ни разу не применял золотое сечение. Ситуация резко переменилась после выхода в свет уже упоминавшегося авторитетного труда Матилы Гика «Эстетика пропорций в природе и искусстве», а с появлением в 1931 году его «Золотого сечения» мистические аспекты φ стали волновать читающую публику еще сильнее. Ле Корбюзье увлекся «Эстетикой» и золотым сечением по двум причинам. С одной стороны, это было следствием его интереса к основным геометрическим формам и структурам, скрытым за природными явлениями. С другой стороны, в семье Ле Корбюзье приветствовали музыкальное образование, и он вполне мог оценить пифагорейское стремление к гармонии, достигаемой соотношениями чисел. Он писал: «Более тридцати лет назад по жилам моих работ – и архитектурных, и живописных – заструился сок математики, ибо музыка никогда меня не покидает». Поиски стандартизированной пропорции достигли пика в создании новой системы пропорций – Модулера.

Предполагалось, что Модулер станет «гармонической мерой человеческого масштаба, применимой универсально в архитектуре и в механике». В сущности, такое определение – не более чем перефразированное знаменитое изречение Протагора, высказанное в V веке до н. э.: «Человек есть мера всех вещей». Естественно, Модулер был основан на пропорциях человеческого тела (рис. 79) – в духе «Витрувианского человека» (рис. 53) и общей философской задачи создать систему пропорций, эквивалентной той, что создала природа. Человек ростом шесть футов (около 183 см), несколько напоминающий знакомого «мишленовского человечка» с рекламы шин, с поднятой рукой (общая высота составляет 226 см, или 7 футов 5 дюймов), вписан в квадрат (рис. 80). Отношение его роста (183 см, 6 футов) к расстоянию от подошв до пупка (на середине общей высоты – 113 см, 3 фута 8,5 дюймов) – это в точности золотое сечение. Общая высота – от подошв до кончиков пальцев поднятой руки – также делится в золотом сечении (на 140 см и 86 см) на уровне запястья опущенной руки. Два отношения – 113/70 и 140/86 – подразделялись далее на более мелкие величины в соответствии с последовательностью Фибоначчи – каждое число есть сумма двух предыдущих (рис. 81). Окончательная версия Модулера (рис. 79 и 81), таким образом, опиралась на две взаимопроникающие шкалы чисел Фибоначчи («красная и голубая серии»). По предложению Ле Корбюзье Модулер должен был обеспечить гармонические пропорции всему – от размеров дверных ручек и шкафов до зданий и городов. В мире, где постоянно росла потребность в массовом производстве, Модулер должен был предоставить модель для стандартизации. Ле Корбюзье выпустил две книги – «Модулер» (1948) и «Модулер II» (1955) ( Le Corbusier . Le Modulor; Le Corbusier . Modulor II), которые вызвали пристальное внимание в кругах специалистов по архитектуре и до сих пор служат аргументом в любом споре о пропорциях. Ле Корбюзье очень гордился тем, что ему представился случай показать «Модулер» самому Альберту Эйнштейну – они встречались в Принстоне в 1946 году. Вот как архитектор вспоминал этот момент: «Я плохо говорил, плохо рассказал о Модулере, завяз в трясине причинно-следственных связей». Тем не менее, Эйнштейн написал ему письмо, где сказал о Модулере так: «Это шкала пропорций, благодаря которой сделать плохо станет трудно, а сделать хорошо – легко».