Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

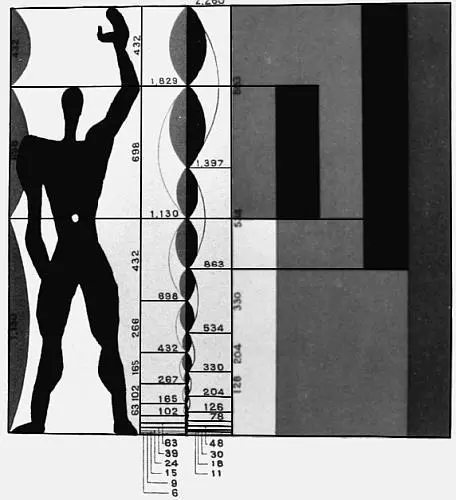
Рис. 79

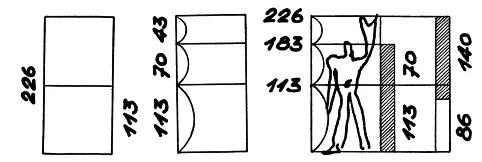
Рис. 80

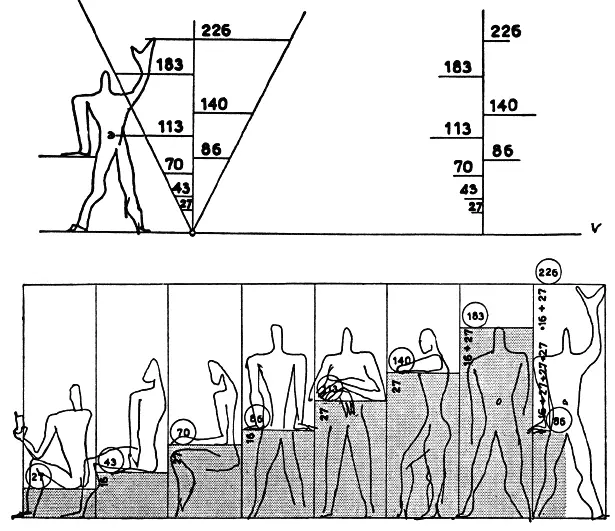
Рис. 81

Свою теорию Модулера Ле Корбюзье воплощал на практике во многих своих проектах. Скажем, в предварительных заметках к проекту целого индийского города Чандигарх, где стоят четыре крупных правительственных здания – парламент, дворец правосудия и два музея – мы читаем: «Однако, разумеется, при разработке ритма окон учитывается Модулер… в общей части здания, где, в частности, многочисленные кабинеты и залы суда должны укрываться от солнца, Модулер обеспечивает единство текстуры. В дизайне фасадов Модулер (с точки зрения текстуры) задействует красную и голубую серию в пределах пространств, уже ограниченных оконными рамами».

Разумеется, художники интересовались золотым сечением и после Ле Корбюзье, однако большинство его последователей увлекались скорее математико-философски-историческими качествами этого соотношения, нежели его предполагаемыми эстетическими свойствами. Скажем, английский абстракционист Энтони Хилл в 1960 году применил последовательность Фибоначчи в параметрах своей работы «Конструктивный рельеф» (рис. 82). Подобным же образом современный израильский художник и скульптор Игаль Тумаркин сознательно включил формулу φ (φ = (1+√5)/2) в одну из своих картин.

Рис. 82

Итальянец Марио Мерц превратил последовательность Фибоначчи в важную составляющую своих работ. Мерц родился в Милане в 1925 году, а в 1967 году примкнул к художественному течению «Арте повера» (итал. « Arte Povera » – «бедное искусство»), куда также входили художники Микеланджело Пистолетто, Лучано Фабро и Яннис Кунеллис. Название движения (его придумал критик Джермано Челант) объясняется стремлением участников применять в своем творчестве простые повседневные материалы в знак протеста против негуманного общества потребления, каким они его видели. Применять последовательность Фибоначчи Мерц начал в 1970 году в серии «концептуальных» работ, куда входили последовательности чисел и разнообразные спирали.

Мерц так стремился применять числа Фибоначчи, поскольку эта последовательность лежит в основе многих закономерностей роста и развития в природе. В своей работе 1987 года под названием «Ударная волна» (« Onda d ’ urto ») художник разместил длинный ряд стопок газет, над каждой из которых сияют неоновые числа Фибоначчи. Работа «Неаполь Фибоначчи» (1970) состоит из 10 фотографий фабричных рабочих, где количество изображенных возрастает в соответствии с последовательностью Фибоначчи от одиночных портретов до группы из 55 человек (десятое число Фибоначчи).

Необоснованные утверждения, что тот или иной художник якобы применял в своем творчестве золотое сечение, множатся, словно грибы после дождя. Одно подобное заявление заслуживает особого разбора, поскольку его без конца повторяют. Голландский художник Пит Мондриан (1872–1944) известен в основном благодаря своему беспредметному геометрическому стилю, который он назвал неопластицизмом. В частности, для композиции многих его картин характерно применение исключительно вертикальных и горизонтальных линий, прямоугольников и квадратов и только основных цветов (иногда – с вкраплениями черного и серого) на белом фоне, как, например, в картине «Буги-вуги на Бродвее» (рис. 83, хранится в Музее современного искусства в Нью-Йорке). Изогнутые линии, трехмерность, реалистичность изображения в его творчестве полностью исключались.

Рис. 83

Наверное, не стоит удивляться, что геометрические композиции Мондриана привлекли пристальное внимание адептов золотого сечения и стали предметом различных спекуляций. Дэвид Бергамини в своей «Математике» признает, что сам Мондриан «толковал композицию своих картин расплывчато», но тем не менее, утверждает, что линейная абстракция «Площадь Согласия» заключает в себе взаимоперекрывающиеся золотые прямоугольники. Шарль Було в своей «Тайной геометрии художника» позволяет себе еще более смелые заявления: он утверждает, что «Французские художники никогда не осмеливались заходить так далеко в чистую геометрию и так строго и последовательно применять золотое сечение, как холодный и безжалостный голландец Пит Мондриан». Далее Було говорит, что в «Буги-вуги на Бродвее» «почти все горизонтали и вертикали, составляющие картину, построены на золотом сечении». Я потратил некоторое время на изучение более серьезных работ о творчестве Мондриана и не нашел там ни единого упоминания о золотом сечении, и тогда мне стало интересно, как же все было на самом деле: применял или не применял Мондриан золотое сечение в композиции своих картин? В отчаянии я решил прибегнуть к последнему средству и обратился к настоящему специалисту. Это был Ив-Ален Буа из Гарвардского университета, соавтор книги «Мондриан» ( Yves - Alain Bois et al . Mondrian), выпущенной в 1999 году к ретроспективной выставке художника. Ответ Буа был совершенно недвусмыслен: «Насколько мне известно, у Мондриана никогда не было никакой системы пропорций, если не считать своего рода сеток из модулей, которые он писал в 1918–1919 годах, но там система выводилась из формата самих картин – восемь на восемь единиц». Далее Буа добавил: «Помнится, и сам Мондриан язвил по поводу того, что в его работах якобы использовались арифметические выкладки». «Думаю, что золотое сечение применительно к Мондриану – чистой воды чушь». Все эти занимательные исторические анекдоты оставляют один нерешенный вопрос. По какой же причине столь много художников задумывались о том, как задействовать золотое сечение в композиции своих работ – если не считать чисто интеллектуального любопытства? Может быть, это соотношение, выраженное в виде золотого прямоугольника, и в самом деле обладает какими-то имманентными эстетическими свойствами, которые ставят его выше других пропорций? Сами по себе попытки ответить на этот вопрос привели к массе психологических экспериментов и написанию множества книг и статей.

Словами, вынесенными в название этого раздела, итальянский философ-схоласт Фома Аквинский (ок. 1225–1274) попытался выразить фундаментальные отношения между математикой и красотой. Похоже, людям доставляют удовольствие «формы», обладающие определенной симметрией или подчиняющиеся определенным геометрическим правилам.