Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

К примеру, мы обнаружили кость доисторического животного, содержащую 1/100 изотопа С-14. Чему равен возраст находки? По условию задачи, с будет равно 100. Подставив это значение в исходное выражение, имеем:

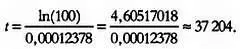
Можно сделать вывод: возраст кости составляет примерно 37 тысяч лет.

В 1798 году Томас Роберт Мальтус опубликовал книгу «Эссе о росте народонаселения». Согласно его гипотезе, в какой-то момент численность населения Земли будет расти в геометрической прогрессии, то есть экспоненциально. При этом объем продовольственных и любых других ресурсов возрастает в арифметической прогрессии, то есть линейно. Так, численность населения описывается последовательностью 2 (2 1), 4 (2 2), 8 (2 3), 16 (2 4), 32 (2 5), 64 (2 6) и т. д., количество продовольственных ресурсов — 2, 3, 4, 3, 6 и т. д. Следовательно, наступит момент, когда высокая рождаемость, особенно среди рабочего класса, приведет к недостатку продовольствия (отметим, что марксисты считали теории Мальтуса нападками на рабочий класс).

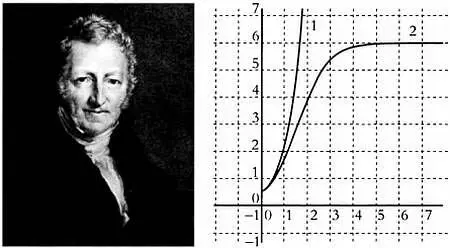
Англиканский священник Томас Роберт Мальтус(1766–1834). Справа представлены две модели роста: экспоненциальная (1) и линейная (2).

Допустим, что мы применили модель Мальтуса, в частности у' = r·у , к некоторой популяции животных или микроорганизмов. В конечном итоге в этой модели скорость роста населения у пропорциональна численности населения у . Таким образом, применив математические методы, можно преобразовать исходное дифференциальное уравнение, как показано ниже. Во-первых, нужно записать уравнение в следующем виде: dy / dt = r·у , где r — параметр, отражающий рост населения с постоянной скоростью, которая не меняется в последующих поколениях. Этот параметр называется коэффициентом роста населения.

Затем перенесем dt в правую часть так, что d y = r · y · dt . Это уравнение словно подсказывает, что нужно сгруппировать в одной части все члены, связанные с у . Следовательно, перенесем у в левую часть. Имеем dy / у = r · dt .

Наконец, чтобы решить уравнение, нужно взять интеграл от обеих его частей, как показано далее:

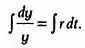
На этом этапе у читателя может создаться впечатление, что мы не решаем задачу, а только усложняем рассуждения. Внимательно рассмотрим выражение. В правой его части записан простейший табличный интеграл. Так как r — константа, ее можно вынести за знак интеграла. Имеем:

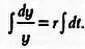
Напомним, что 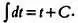Правая часть равенства будет выглядеть так:

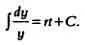
В левой части также записан табличный интеграл. Обратите внимание, что, поскольку dy записано в числителе, у — в знаменателе, интеграл будет равен логарифму у , а именно:

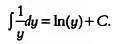
Поэтому

ln( y ) = r · t + C .

Если мы избавимся от логарифма и сгруппируем члены выражения, то найдем решение дифференциального уравнения у' = r · у . Для этого подставим в выражение величину, обозначающую исходное число бактерий (ранее мы обозначили его через у 0 ). Определим функцию у :

y = y 0 e rt

В 1838 году математик Пьер Франсуа Ферхюльст видоизменил модель Мальтуса с учетом того, что размеры окружающей среды ограничены, поэтому должно существовать некоторое максимальное значение численности населения k , известное как поддерживающая емкость среды. Ферхюльст получил следующее дифференциальное уравнение: у' = r · y ( k — у ).

Бельгийский математик Пьер Франсуа Ферхюльст(1804–1849), один из величайших специалистов по теории чисел первой половины XIX века.

Решением уравнения Ферхюльста является знаменитое логистическое уравнение, которое описывает не только рост населения, но и распространение эпидемий и рост социальных сетей в интернете:

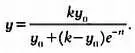
Логистическое уравнение применимо для анализа S-образного роста — экспоненциального, но ограниченного количеством ресурсов, будь то физическое пространство, продовольствие, емкость рынка мобильной связи или число пользователей социальной сети. Экспоненциальный рост является неограниченным, то есть утопичным, возможным только в мире с неисчерпаемыми ресурсами. В логистической же модели рассматривается реальный мир, к примеру планета Земля, ресурсы которой, что очевидно, ограничены.

Любопытно отметить, что эти модели были предложены в XIX веке, в разгар промышленной революции. В эту эпоху жили такие ученые, как Чарльз Дарвин, создатель теории эволюции путем естественного отбора, и Чарльз Бэббидж, изобретатель аналитической и разностной машин — прообразов современных компьютеров. Эти любопытные совпадения предвосхитили плодотворный союз математики и компьютерных технологий, который сыграл в XX веке определяющую роль в изучении жизни.

Биотехнология — это раздел биологии, с помощью которого методы генной инженерии и выращивания клеточных культур находят широкое применение в сельском хозяйстве, фармакологии, медицине и диетологии. Основной инструмент биотехнологов — хемостат, резервуар или биореактор, в котором посредством культивирования клеток вырабатываются полезные вещества.

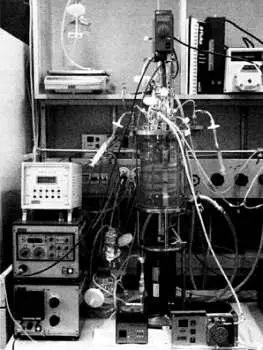
Биореактор в лаборатории. Внутри биореактора находятся клетки.

Цель подобных исследований — достичь состояния, при котором число микроорганизмов N и объем питательных веществ С были бы практически постоянными, а рост численности микроорганизмов — экспоненциальным. Именно при таком росте вырабатываются полезные вещества, например антибиотики. В ходе эксперимента необходимо постоянно пополнять запас питательных веществ и одновременно убирать жидкости, токсины и любые другие продукты метаболизма микробов, при этом объем среды культивации должен оставаться неизменным. В промышленности хемостаты используются для выработки этанола, ферментированных продуктов питания (например, сыров), белков, обладающих лечебными свойствами (в частности, инсулина), и т. д. Хемостаты также применяются при изучении экологии микроорганизмов, а также для анализа их эволюции.