Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

Как вы уже, наверное, догадались, инженеры-биохимики и другие специалисты в сфере биотехнологий в своих экспериментах с биореакторами успешно и широко применяют дифференциальные уравнения, которым посвящен отдельный раздел математической биологии. К примеру, дифференциальные уравнения, описывающие процессы, происходящие в хемостате, выглядят так:

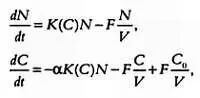
где N — число микроорганизмов, С — концентрация питательных веществ, F — поток (при этом F вход = F выход ), V — объем. В дифференциальных уравнениях К( С ), α и C 0 — параметры модели. Обратите внимание, что первое дифференциальное уравнение, описывающее изменение N , напоминает логистическое уравнение (о нем мы поговорим позже). Оно также содержит поток F . На основе этих и других выражений были разработаны программы, управляющие хемостатами, которые используются, в частности, для компьютерного контроля ферментации.

Математическое изучение рака: опухоли в компьютере

Рак — это заболевание, при котором наблюдается бесконтрольный рост группы клеток, образующих опухоль, разрушающую близлежащие клетки и ткани (это определение не вполне подходит для лейкемии). В действительности раковая опухоль содержит и обычные клетки, злокачественная трансформация которых ведет к образованию раковых. Поскольку рак чрезвычайно распространен, он стал одним из объектов изучения математической биологии. Лечение раковых заболеваний настолько важно, что сегодня существует целая база данных QCDB (от англ. Quantitative Cancer Modelling DataBase — «база данных для количественного моделирования рака»), предоставляющая доступ к информации об этом заболевании биоматематикам всего мира.

Математическое изучение раковых заболеваний проводится с использованием математических моделей и компьютерного моделирования. Математика при этом, во-первых, помогает выдвигать новые гипотезы о причинах образования опухолей, а во-вторых, использование математических моделей позволяет лучше проанализировать огромные объемы накопленных экспериментальных и клинических данных.

Биологи и математики рассматривают опухоли как сложные системы. Раковые клетки в них взаимодействуют между собой и с другими клетками, при этом их поведение нельзя объяснить, если мы будем рассматривать раковые клетки изолированно от других. Согласно этому подходу, предполагается, что опухоль образуется не в результате сбоя в конкретном гене. Причиной рака является общий сбой взаимодействия между генами. Проводя параллель с интернетом, рак можно считать результатом нарушения работы множества компьютеров в сети (DNS-серверов, маршрутизаторов и т. д.), а не результатом сбоя какого-то конкретного компьютера.

В 1964 году исследователь по фамилии Лэйрд заметил, что рост опухолей в условиях ограниченного пространства и питательных веществ описывается функцией Гомпертца. Классическим примером является рак груди. Скорость роста опухоли в этих условиях, у' (размер опухоли может быть выражен через ее объем или число клеток), описывается следующим дифференциальным уравнением:

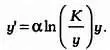
В этом выражении α — параметр, описывающий способность раковых клеток опухоли к росту, К — максимально возможный размер опухоли (напомним, что объемы ткани, в которой находится опухоль, и количество питательных веществ ограничены). Решением этого дифференциального уравнения будет функция Гомпертца, предложенная английским математиком Бенджамином Гомпертцем в 1825 году как уточнение модели Мальтуса. Функцию Гомпертца первыми применили страховые компании. Основная ее идея заключается в том, что с увеличением возраста уровень смертности возрастает в геометрической прогрессии.

Гомпертц описал любопытную связь между уровнем смертности, который мы обозначим через R m , и возрастом t :

R m = R 0e βt + A

Особенность этого выражения заключается в том, что А играет удивительную роль: эта величина отражает воздействие на уровень смертности факторов, не связанных с возрастом человека. К примеру, рост средней продолжительности жизни в развитых странах обусловлен именно тем, что удалось значительно снизить значение А благодаря росту уровня жизни и созданию более здоровой среды. На снижение А могли повлиять рост городов, появление зданий, защищенных от воздействия климата, улучшение гигиены, питания и т. д. Тем не менее параметр β остается неизменным. Сердечные и раковые заболевания стали причиной того, что, с одной стороны, R m в результате снижения А уменьшилось, но, с другой стороны, с возрастом R m увеличивается. Дастся ли нам когда-нибудь устранить или существенно снизить воздействие возраста, или t , на R ?

Если мы используем функцию Гомпертца в ином контексте, в частности применительно к раковым заболеваниям, то размер опухоли у будет описан выражением:

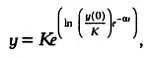
где у(0) — начальный размер опухоли. Если пациент проходит лечение, то у(0) будет меньше К , в противном случае размер опухоли будет увеличиваться.

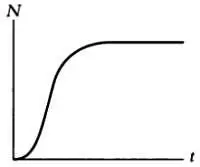
Кривая Гомпертца, описывающая рост раковой опухоли ( N— размер опухоли, t— время).

Эта функция весьма схожа с сигмоидой (логистической функцией): рост опухоли замедлен в начале и конце процесса. Замедление в конце процесса кажется очевидным, если учесть, что по мере роста опухоли клетки, расположенные внутри нее, получают меньше кислорода, отмирают и вызывают некроз ядра опухоли. В результате ее размер стабилизируется: рост внешней части уравновешивается отмиранием клеток во внутренней части.

Этому же закону подчиняется и динамика роста некоторых предприятий, в частности тех, где большую роль играют технологии, — фармацевтических компаний или операторов мобильной связи. Вначале затраты на исследования, патенты и т. д. превышают доходы от продаж, затем компания переживает период бурного роста и получает прибыль. На следующем этапе продажи падают, так как рынок постепенно насыщается. Также функцией Гомпертца описывается рост органов эмбриона или, что еще любопытнее, регенерация хвоста у ящерицы.

Хотя приведенное выше выражение может показаться сложным, следует понимать, что благодаря компьютерам вычислить его значение сравнительно легко. По сути, речь идет о достаточно простом выражении вида 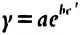, в котором показатель степени возводится в новую степень.