Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

В 1980-е годы исследователь Уэлдон заметил, что этой функцией не очень точно описывается рост опухолей малых размеров, поскольку в ней не учтены некоторые биологические аспекты, в частности роль иммунной системы. В поправке Уэлдона утверждается, что на первом этапе роста опухоли раковые клетки не сражаются за доступные ресурсы, и их рост описывается экспоненциальным законом, или моделью Мальтуса. Однако по достижении некоторого критического размера рост опухоли будет описываться уже не моделью Мальтуса, а функцией Гомпертца.

* * *

МАТЕМАТИКА И НОВЫЕ ПУТИ ИССЛЕДОВАНИЯ

В 2005 году исследователь Антонио Бру из мадридского университета Комплутенсе предположил, что на поздних стадиях раковые заболевания можно излечивать, вызывая сильное и продолжительное воспаление тканей вокруг опухоли. Эта гипотеза стала результатом математических исследований роста раковых клеток. В ходе исследований было отмечено, что рост всех клеток подчиняется одной схеме, которую Бру назвал схемой универсальной динамики роста опухолей. В этой модели клетки на границе опухоли играют определяющую роль в методе лечения, предложенном Бру. Первоначальное скептическое отношение к гипотезе отчасти было вызвано тем, что использованная математическая модель отличалась от классических моделей раковых заболеваний. Во-первых, в ней предполагалось, что рост клеток подчиняется не экспоненциальному, а линейному закону, а во-вторых, считалось, что рост опухоли зависит не от количества питательных веществ, а от свободного пространства. Это прекрасный пример того, как математика подсказывает исследователям новые пути лечения рака.

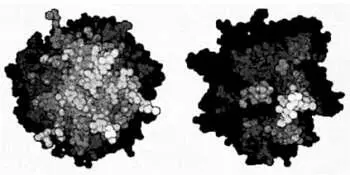
Математическая модель и результат компьютерного моделирования роста раковой опухоли.

* * *

СПИД, свиной грипп и другие заболевания, которые можно изучить с помощью математики

В 1983 году французский исследователь Люк Монтанье описал вирус СПИДа, или ВИЧ (вирус иммунодефицита человека). Он представляет собой сферу диаметром 100 нанометров и имеет внешнюю белковую оболочку. Вирусологи называют этот вирус ретровирусом, так как его геном образован цепочкой РНК. По данным Всемирной организации здравоохранения, в 2006 году в мире насчитывалось примерно 39,3 миллиона человек, зараженных вирусом СПИДа, примерно 24 миллиона из них проживали на Африканском континенте.

В 2009 году средства массовой информации сообщили о начале пандемии свиного гриппа. По данным Всемирной организации здравоохранения, возбудителем заболевания является вирус H1N1/09. Его геном представляет собой смесь ДНК птиц, свиней и человека, поэтому вирус способен преодолевать межвидовые барьеры. Свиной грипп был самой популярной темой в СМИ летом и осенью 2009 года. Изначально процент смертельных случаев среди заболевших был высоким, однако со временем он снизился, что совпало с началом широкого использования противовирусных препаратов.

Подобные заболевания, носящие характер пандемии, становятся источником напряженности в обществе. Как санитарные службы всего мира прогнозируют и отслеживают распространение заболеваний? Как определяется момент начала эпидемии в определенной стране? Когда следует начинать вакцинацию людей, входящих в группу риска? Ответы на эти вопросы дает ряд математических моделей, составляющих формальное ядро эпидемиологии, которая изучает факторы, влияющие на здоровье и заболеваемость населения. Эпидемиология привлекла внимание математиков еще в начале XX века, а сегодня она стала одной из областей изучения математической биологии.

Первыми, кто рассмотрел эпидемии с точки зрения математики, были Уильям Хаммер и Рональд Росс. Для анализа эти ученые применили закон действующих масс. Позднее Лоуэлл Рид и Уэйд Фрост разработали модель Рида — Фроста, связав число здоровых людей, восприимчивых к заболеванию ( S ), число заболевших ( I ) и число людей, невосприимчивых к заболеванию.

Анализировать распространение заболеваний специалистам вновь помогают дифференциальные уравнения. Допустим, что численность населения составляет N человек, из которых I заражены вирусом. Это означает, что число здоровых людей равно N — I . Так как люди, зараженные вирусом, живут рядом со здоровыми, последние подвергаются риску заражения ( S ). Следовательно, S = N — I .

В одной из классических моделей эпидемиологии утверждается, что изменение числа зараженных в зависимости от времени описывается дифференциальным уравнением: I' = k · I ·( N — I ). В упрощенном виде оно выглядит так: I' = k · I · S . Решением этого дифференциального уравнения будет знаменитое логистическое уравнение, описывающее ход любой эпидемии:

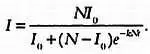
Обратите внимание, что в начале эпидемии (то есть при t , стремящемся к нулю) логистическое уравнение будет приблизительно эквивалентным уравнению экспоненциального роста, то есть уравнению модели Мальтуса. Это отражает тот факт, что в начале эпидемии число зараженных резко увеличивается. В случае с заболеваниями, которые становятся причиной напряжения в обществе, например СПИДом или свиным гриппом, сообщения о росте эпидемии, распространяемые СМИ, только усугубляют панику.

Если предположить, что предельное число заболевших равно числу здоровых людей, восприимчивых к заболеванию, то есть N, то начиная с определенного момента рост эпидемии замедлится, как и рост числа новых заболевших, I . Это значение, столь важное для органов здравоохранения любой страны, достигается, когда число заболевших I составляет половину численности восприимчивого к вирусу населения, то есть N /2. После этого количество новых случаев заболевания стабилизируется вплоть до окончания эпидемии.

В настоящее время благодаря использованию компьютерного моделирования можно оценить распространение эпидемии (например, сезонного гриппа), что позволяет органам здравоохранения формировать календарь вакцинации населения.

В эпидемиологии используются такие компьютерные программы, как Epigrass, Any Logic Model-Builder и STEM ( Spatio Temporal Epidemiological Modeler ).

Число e и колония бактерий Escherichia coli

Нет такой области науки, где рано или поздно не появилось бы число е , будь то молекулярная биология или статистика, физика или химия. Это вездесущее число обнаруживается во множестве природных явлений. Число е — иррациональное. Это означает, что его десятичная запись никогда не заканчивается и не повторяется, что роднит его с числом π . Считается, что число е открыл Якоб Бернулли при изучении следующего предела: