Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

* * *

Одна из классических математических задач звучит так. Предположим, что мы хотим найти неизвестную функцию у , для которой известна ее производная у' . Допустим, производная у' неизвестной функции у равна З х 2(говоря математическим языком, у' = 3 x 2). Необходимо определить у . Эта задача допускает несколько возможных решений (они называются первообразными), но если нам также известно значение функции в некоторой точке, например у(0) = 0, то решение будет единственным. Чтобы найти у, нужно вычислить интеграл .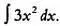

Сначала вынесем число 3 за знак интеграла: 3· Затем, поскольку мы имеем дело с табличным интегралом, достаточно вспомнить следующую формулу:

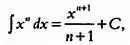
где С — константа интегрирования. В нашем случае функция у выглядит так:

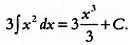
В нашем случае С = 0, так как у(0) = 0. Упростив выражение, получим искомую функцию: у = t 3. Задача была успешно решена стандартными методами интегрального исчисления.

Что произойдет, если производная у не будет напрямую выражена в виде f( t ), нужно найти? Именно так выглядят дифференциальные уравнения, в которых значение у' связано со значением у . Производная функции по времени обозначается у' либо dy / dt . Эти обозначения эквивалентны. В простейших случаях дифференциальное уравнение имеет следующий вид:

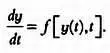
Расскажем немного подробнее об элементах дифференциального уравнения. Что означает у' , или dy / dt ? Производная выражает уровень изменений, скорость или ритм изменения системы. Напомним, что одной из характеристик динамических систем является зависимость их состояния от взаимодействия между их элементами, при этом любое изменение произвольного элемента влияет на общее состояние системы у . Иными словами, если известно состояние системы в момент времени t , например у(t), и мы подставим это значение в дифференциальное уравнение, то определим степень изменений системы — она будет характеризоваться значением у' . Заметьте, что дифференциальные уравнения в силу своих свойств наиболее удобны для построения математических моделей динамических систем и поэтому играют важную роль в математической биологии — с их помощью были успешно смоделированы многие биологические и экологические явления, о которых мы расскажем в этой главе.

Но как найти у в дифференциальном уравнении? Эта задача в общем виде решается не так просто, как в предыдущем примере, когда, зная производную функции у' = З х 2, мы смогли вычислить саму функцию. В дифференциальных уравнениях наряду с у' фигурируют и другие члены.

Если сравнить дифференциальное уравнение с шоколадным пасхальным яйцом, внутри которого находится игрушка, то решение уравнения будет равносильно тому, чтобы извлечь игрушку путем последовательных действий. К примеру, сначала нужно снять с яйца обертку, затем съесть шоколад, и только тогда вы увидите игрушку или, в случае с дифференциальным уравнением, найдете искомую функцию у . Следовательно, решить дифференциальное уравнение означает найти функцию у . Если выполнить с этим уравнением различные действия, вы получите и, если возможно, примените аналитические методы решения. На одном из этапов решения мы используем интегральное исчисление, однако не столь явно, как в предыдущем примере.

Пример решения представлен в следующей главе для уравнения модели Мальтуса, которое играет основную роль в демографии и при изучении динамики популяций. Если методы интегрального исчисления заведут нас в тупик, мы также сможем найти приближенное решение с помощью компьютера. Приближенное решение означает, что мы выберем желаемую точность результата и применим алгоритм, который позволит найти решение с точностью, превышающей указанную. Теория численного анализа гарантирует, что определенный алгоритм позволяет найти решение с наперед заданной (или более высокой) точностью.

Наиболее известные численные алгоритмы решения дифференциальных уравнений — это метод Эйлера и метод Рунге — Кутты. Эти методы используют не только математики, но и экологи, а также сотрудники фармакологических лабораторий. Метод Рунге — Кутты более известен и обеспечивает прекрасное соотношение между временем расчетов на компьютере и точностью результата. Метод Эйлера проще, но менее точен.

Дифференциальное уравнение Парка юрского периода

В 1950-е годы Уиллард Либби разработал интересный метод определения примерного возраста ископаемых. В основе метода Либби лежало измерение содержания радиоактивного изотопа углерода С-14 в изучаемом объекте, например, в ископаемом или в Туринской плащанице.

Американский химик Уиллард Либби(1908–1980) на обложке журнала Time.

С-14 — это изотоп углерода, концентрация которого в атмосфере Земли постоянна. Живые организмы в течение жизни накапливают углерод С-14, получая его с дыханием и при питании другими живыми существами. Каким бы путем С-14 ни попадал в организм, его содержание также будет неизменным. После смерти накопление С-14 прекращается, и его концентрация в тканях начинает постепенно снижаться.

Чтобы получить формулу для определения возраста объектов, используем уравнение роста из модели Мальтуса. Обозначим через у содержание С-14 в определенный момент времени t , через у 0 — содержание С-14 в ископаемом. Кроме того, искомая формула будет включать r — так называемую константу распада, известную для всех изотопов: у = y 0e rt .

Так как известно, что период полураспада С-14 составляет 5600 лет, предыдущее выражение примет вид:

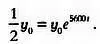
После ряда преобразований получим у = у 0е -0,00012378 t . Выразив время t из этого выражения, найдем формулу, с помощью которой палеонтологи и археологи определяют возраст ископаемых и археологических находок:

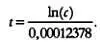
Это выражение можно использовать в случаях, когда возраст анализируемого объекта не превышает 50 тысяч лет.