Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

Эта дисциплина возникла в 2005 году, ее цель — создание моделей, объясняющих биологические явления, при этом большую важность имеет биологическая задача, а не математические преобразования символьных выражений. В настоящее время алгебраическая биология считается частью биологии систем и используется для анализа и моделирования биологических систем при создании моделей биохимических реакций, регулировании экспрессии генов, а также для решения различных задач клеточной и молекулярной биологии.

Также алгебраическая биология применяется в эпидемиологии, при изучении популяций организмов и решения таких задач, как построение филогенетических деревьев, показывающих эволюционные взаимосвязи между различными видами. Не вдаваясь в детали, отметим, что с помощью этой дисциплины удалось создать модель одного из известнейших механизмов молекулярной биологии — лактозного оперона бактерии Escherichia coli , который был открыт Франсуа Жакобом и Жаком Моно (Нобелевская премия по медицине 1965 года). Чем может быть полезна вычислительная модель чего-то, открытого еще в 1960-е? Дело в том, что вычислительная алгебра — это относительно новый и очень мощный инструмент, позволяющий создавать биологические модели и системно анализировать их. И в этом случае речь идет не об открытиях, а о методе, позволяющем исследователям яснее понять все составляющие сложного механизма лактозного оперона и даже поиграть с ними.

Последний раздел этой главы посвящен четырем важным примерам использования математики в биологии. Мы поговорим о матрице Лесли, клеточных автоматах, модели «хищник — жертва» и клеточных автоматах, а также о применении теории множеств в математической модели иммунной системы. Изучение популяций оленей, белок и других животных.

Матрица Лесли

Патрик Лесли родился в 1900 году. Он был экологом и работал в Оксфорде, в организации, занимавшейся подсчетом численности животных. В 1945 году Лесли опубликовал модель структуры популяции, которая нашла широкое применение в экологии популяций и демографии. Эта модель позволяет определить рост популяции с учетом ее возрастной структуры. Сведя воедино две функции (первая описывала рождаемость, вторая — уровень смертности), ученый определил матрицу популяции, известную под названием матрицы Лесли. Эта матрица является квадратной, то есть имеет одинаковое число строк и столбцов, совпадающее с числом составляющих некоторого вектора. Также в этой модели предполагается, что популяция является изолированной и не пополняется в результате миграции. Поскольку модель применяется для животных, которые размножаются половым путем, в ней учитываются только самки: число самцов на рост популяции не влияет. Составляющие вектора, о котором мы упоминали выше, обозначают число особей определенного возраста.

Объясним модель Лесли на следующем примере. Предположим, что в природной среде, например в национальном парке или заповеднике, была зафиксирована следующая численность самок оленей, которые в момент времени t (связанный, к примеру, с датой выборки) принадлежали к возрастным группам под номерами 0, 1, 2, 3 и 4: N 0 t, N 1 t, N 2 t, N 3 t и N 4 t . Обратите внимание, что 0, 1, 2, 3 и 4 — всего лишь обозначения, указывающие возрастные интервалы, к примеру в годах, от меньшего возраста к большему. В нашем примере предполагается, что оленей можно разделить на пять возрастных групп согласно ожидаемой продолжительности жизни.

Также предполагается, что плодовитость всех особей известна, то есть экологи, работающие в заповеднике, знают среднее число детенышей у самок определенного возраста. Если рассмотреть всю популяцию, то число новорожденных оленей, которые включаются в возрастную группу, образованную самыми молодыми особями в следующем поколении (то есть в момент времени t + 1), будет равно:

N 0 t+1 = f 0N 0 t + f 1N 1 t + f 2N 2 t + f 3N 3 t + f 4N 4 t

Теперь будем учитывать смертность оленей, вызванную различными причинами. В этом случае особь не перейдет из текущей возрастной группы в следующую, так как не достигнет нужного возраста. Обозначим через s 0, s 1, s 2 и s 3 долю выживших особей в каждой возрастной группе, которые, таким образом, перейдут в следующую возрастную группу. Это число выражается в долях единицы и обозначает вероятность. Как следствие, в рассматриваемой модели число самок, перешедших в следующую возрастную группу, определяется формулой N 1 t+1 = s 0N 0 t, N 2 t+1 = s 1N 1 t, N 3 t+1 = s 2N 2 t и N 4 t+1 = s 3N 3 t . В математической биологии модель Лесли иллюстрирует очень элегантную и оригинальную формулировку. Все представленные выше выражения сведены в матрицу перехода L , которая получила название матрицы Лесли:

Представим в виде вектора N для поколения t число самок в каждой возрастной группе, то есть N 0 t, N 1 t, N 2 t, N 3 t и N 4 t :

Представим в виде вектора N t + 1 число самок в каждой возрастной группе для следующего поколения, t +1:

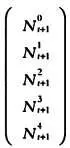
В конце концов объединим матрицу L и векторы N t и N t + 1описанные выше, в одно выражение в матричной нотации. Сразу же увидим, что для получения возрастной структуры популяции, начиная от поколения t и заканчивая следующим поколением, t + 1, достаточно найти произведение вектора, соответствующего поколению t , и матрицы L :

В сокращенном виде это записывается так: N t + 1 = L · N t .

Не описывая пока подробности выполнения операций над матрицами (об этом мы поговорим в главе 4), предположим, что экспериментальные данные о возрастах популяции оленей таковы: 190, 80, 56, 18 и 6 (численность особей от меньшего возраста к большему). Матрица L будет выглядеть следующим образом:

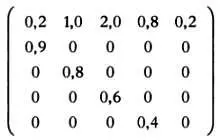
Если мы умножим вектор с исходными данными на матрицу L , получим следующий вектор:

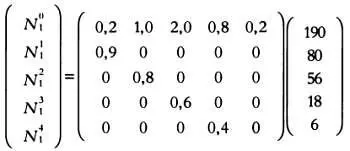
Если мы умножим полученный вектор на матрицу L , получим новый вектор, который затем вновь умножим на матрицу L , и т. д. По прошествии 10 единиц времени, рассчитав последовательные итерации модели, получим, что общая численность популяции будет разделена по возрастным группам (от меньшего возраста к большему) в следующей пропорции: 48, 29, 16, 6 и 4 %.