Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

y' = r · y ·(1 — y ).

Перед тем как рассмотреть уравнение подробнее, выполним последнее действие: заменим у' на y ·( t + 1), у — на у( t ). Эти величины обозначают численность бактерий в момент времени t + 1 в будущем и в настоящий момент времени t соответственно. Теперь исходное дифференциальное уравнение приняло вид:

у( t + 1) = r · у( t )·(1 — у( t )).

Именно это выражение использовал биолог Роберт Мэй в 1976 году при компьютерном моделировании роста популяций.

Четыре эксперимента в качестве примера

Допустим, что микробиолог проводит четыре эксперимента на компьютере. Обозначим их 1, 2, 3 и 4. Показатель мгновенного роста r составит 0,4; 2,4; 3,0 и 3,6 соответственно. Во всех экспериментах исходная численность бактерий у(0) одинакова.

Будем считать, что начальное число бактерий составляет 70 % от их максимальной численности в сосуде, то есть 1. Следовательно, у(0) будет равно 0,7. Обратите внимание, что в каждом из четырех экспериментов будет применяться разное значение r , позволяющее определить численность бактерий у( t +1) для каждого момента времени t .

Графики, соответствующие экспериментам с бактерией Escherichia coli. Слева направо: эксперимент № 2 ( r = 2,4), эксперимент № 3 ( r= 3,0) и эксперимент № 4 ( r= 3,6).

Выполним эксперимент № 1 со значением r = 0,4. Сначала определим численность бактерий по прошествии единицы времени: у(1) = 0,4· у(0)·(1 — у(0)), подставив значение у(0) = 0,7. Найдя у(1), определим численность бактерий по прошествии двух единиц времени у(2): у(2) = 0,4· у(1)·(1 — у(1)). Далее вычислим у(3), у(4) и т. д. вплоть до сколь угодно большого t . К примеру, изучим рост популяции вплоть до t = 100. В этот момент времени численность бактерий будет равна у(100).

Наконец, представим на графике число бактерий у( t ) для каждого момента времени t . Заметим, что для данного начального значения численности бактерий у(0) и определенного значения параметра r с помощью компьютера можно получить значения численности бактерий в разные моменты времени, то есть у(0), у(1), у(2)…, у(100). Эта последовательность чисел называется орбитой. Зададимся вопросом: куда будет направлена эта орбита? Иными словами, каким будет окончательное значение численности популяции?

Чтобы ответить на этот вопрос, проведем все эксперименты согласно вышеописанному принципу, выполнив необходимые расчеты для соответствующих значений r .

В эксперименте № 1 бактерии вымрут: по прошествии определенного времени в сосуде не останется ни одной бактерии. Однако с математической точки зрения популяция достигнет равновесия — это происходит, когда численность популяции не меняется, то есть уровень ее изменения у' , или, что аналогично, dy / dt , будет равен 0.

В нашем эксперименте численность популяции достигла так называемого точечного аттрактора у = 0, то есть популяция бактерий вымерла. Это одно из возможных состояний, к которому может прийти любая популяция. Аттрактор — не более чем точка или множество точек, к которым стремится или приближается динамическая система, в нашем эксперименте это орбита, образованная значениями численности бактерий. Равновесие означает, что система достигла аттрактора и находится в стабильном состоянии, так как dy / dt = 0. Значение у при этом совершенно неважно.

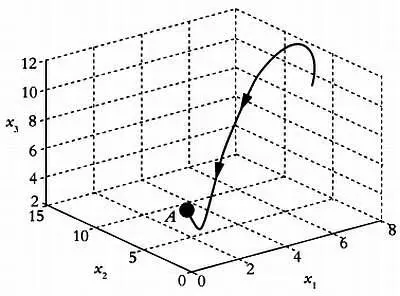
Точечный аттрактор.

Участь популяции бактерий в эксперименте № 2 будет не столь печальной. Эта популяция также достигнет точки равновесия, однако численность бактерий зафиксируется в точечном аттракторе у = 0,6. В эксперименте № 3 численность бактерий будет колебаться между определенным максимальным и минимальным значениями в зависимости от того, в какой момент времени t производится подсчет численности. В этом случае также говорят, что система достигла равновесия.

Эта разновидность аттрактора называется предельным циклом. Речь идет о замкнутой орбите, характерной для систем, в которых наблюдаются колебания. С геометрической точки зрения аттрактор действует подобно сточной трубе. Он может представлять собой точку, кривую или даже фрактал. Следовательно, стабильные системы, к примеру, рассматриваемая колония бактерий, — это системы, которые по прошествии определенного времени стремятся к некоторому аттрактору, в то время как нестабильные системы от аттракторов удаляются.

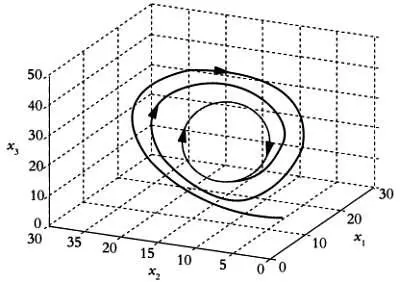
Предельный цикл.

Что же произойдет в последнем, четвертом эксперименте? Сразу же видно, что колебания численности популяции не подчинены никакой закономерности и являются абсолютно хаотическими. В подобных случаях определить точную численность бактерий невозможно: она заметно отличается в зависимости от того, в какой момент мы производим подсчет. Кроме того, в отличие от первых трех экспериментов, в этом случае изменение численности бактерий не подчиняется какой-либо схеме. Можно сделать вывод: хаос есть отсутствие закономерности колебаний. Подобное поведение наблюдается при достижении критического значения параметра дифференциального уравнения. В нашем эксперименте этим критическим значением является r = 3,6.

В этом случае орбита значений численности бактерий у(0), у(1), у(2)…, у(100) приближается к так называемому странному аттрактору. Он описывает поведение таких динамических систем, как климат на Земле, поведение биржевых индексов или электроэнцефалограмма человека.

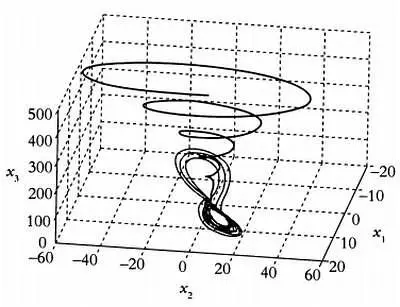
Странный аттрактор.

В предыдущей главе вы познакомились с тем, как математическая биология изучает биологические системы и явления с помощью дифференциальных уравнений. Однако их использование — не единственный метод изучения динамических систем, а следовательно, не единственный метод моделирования биологических явлений. Ввиду все более широкого использования компьютеров еще одним популярным методом являются функции, или отображения. Их применение кажется более простым, чем использование дифференциальных уравнений. Классическим примером является ло