Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

Палитра цветов программы Fractint

* * *

Этими свойствами обладают все фракталы, созданные математиками. Иными словами, фракталы, сгенерированные на компьютере, — это идеальные математические объекты, в отличие от неидеальных фракталов конечного размера, созданных природой. И все же красота и сложность фракталов в природе не перестают удивлять нас.

Снежинка (иллюстрация Уилсона Бентли) и соответствующий ей фрактал — снежинка Коха.

Множества Жюлиа и Мандельброта

Французский математик Гастон Жюлиа первым начал исследовать фракталы. Он сделал ряд важных открытий, однако умер в 1978 году, так и не став известным. Отчасти это объяснялось тем, что компьютеры в то время еще не могли изобразить всю красоту и кажущуюся сложность фракталов. Жизнь Жюлиа вообще сложилась непросто: в Первую мировую войну он был ранен в лицо и вынужден был всю жизнь скрывать его часть.

Фрактальное множество Жюлиа.

Рассмотрим функцию вида Z n+1 = Z n 2+ С , где Z — переменная, С — константа. Значение левой части этого выражения на итерации n + 1 равно квадрату переменной Z на предыдущей итерации, n , увеличенному на константу С . Само по себе это выражение не представляет особого интереса, если только переменная Z и константа С не являются комплексными числами. Именно этот случай и рассмотрел Жюлиа. Несколько лет спустя Бенуа Мандельброт также изучил этот класс итеративных выражений с помощью компьютера. В некотором роде Мандельброт продолжил исследование фракталов, начатое Гастоном Жюлиа, и внес огромный вклад в их популяризацию. В 1958 году Мандельброт начал работать в исследовательском центре IBM в США, где изучал возможности использования фракталов не только в физике, но и в других дисциплинах: гидродинамике или даже экономике. Именно он в 1975 году ввел термин «фрактал» для обозначения подобных объектов. Изучив множества Жюлиа с помощью компьютера, Мандельброт обнаружил множества, которые теперь носят его имя — множества Мандельброта.

Фрактал Мандельброта.

В 1982 году была опубликована книга Мандельброта под названием «Фрактальная геометрия природы», в которой он объяснил, как природа создает фрактальные формы (к примеру, линии побережий, горы, растения, кровеносные сосуды и легкие). На множествах Мандельброта рассматривается орбита точки 0. Ученый предложил изучить последовательные итерации выражения Z n+1 = Z n 2+ С для частного случая Z 0 = 0. Его идея заключалась в том, чтобы определить, каким в этих условиях будет множество значений С , для которых рассматриваемая орбита точки не будет уходить в бесконечность. Именно это множество значений и стало называться множеством Мандельброта. На множествах Жюлиа, напротив, комплексная константа С имеет фиксированное значение, для которого изучается поведение функции, орбита и значения Z 0, Z 1, Z 2 … и т. д. Поскольку компьютер не может работать с комплексными числами, переменная и константа записываются в следующем виде:

Z = X + iY

С = р + iq ,

а функция Z n+1 = Z n 2+ С раскладывается на вещественную часть X и мнимую часть Y .

Компьютер позволяет представить точки орбиты на комплексной плоскости, то есть в декартовой системе координат, и изобразить точки, для которых выражение √( x 2+ Y 2) меньше заданного значения и орбита которых не уходит в бесконечность. Эта орбита является границей множества точек, орбиты которых уходят в бесконечность, и это множество называется множеством Жюлиа.

Хаотические системы представляют собой разновидность динамических систем, что доказал преподаватель Технологического института Джорджии Майкл Барнсли, объяснявший теорию хаоса на примере математической игры под названием «Игра в хаос». Барнсли показал любопытную особенность хаотических систем: их беспорядочность была лишь кажущейся, и в конечном итоге в хаотической системе можно было увидеть одну и ту же фигуру. Эта фигура, очевидно, являлась аттрактором, в частности фракталом, однако проявлялась она только на поздних этапах моделирования. Напомним, что аттрактор — это не более чем точка или множество точек, к которым стремится или приближается динамическая система. «Игра в хаос» заключается в графическом представлении точек ( х, у ), которые описываются следующим матричным выражением:

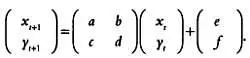
Изначально расположение полученных точек будет казаться случайным. Но ближе к концу эксперимента, после того как мы изобразим достаточное их количество, всегда будет виден странный аттрактор — треугольник Серпинского.

Идея Барнсли была простой, элегантной и в то же время удивительной. Любая точка, которую мы изобразим в будущем, то есть в момент времени t + 1, будет иметь координаты (х t + 1, y t + 1 ). Они будут рассчитаны на основе координат ( x t, у t ) точки, которую мы изобразим в момент времени t . Обратите внимание, что здесь речь идет об отображении, схожем с логистическим отображением или уравнением Ферхюльста. О том, что такое матрицы и как они применяются в математической биологии, поговорим в следующей главе. Пока лишь укажем, что приведенное выше выражение можно преобразовать в два более привычных и определить координаты новой точки на основе следующих преобразований:

х t+1 = aх t + by t + е ,

y t+1 = cx t + dy t + f .

Эксперимент Барнсли заключался в определении трех преобразований.

Для произвольной начальной точки с координатами ( х , у) путем жеребьевки определялось число 1, 2 или 3. К примеру, если при броске кубика выпадало 1 или 2 очка, выбиралось преобразование 1, если выпадало 3 или 4 очка — преобразование 2, если выпадало 5 или 6 очков — преобразование 3. С помощью соответствующих уравнений определялись координаты новой точки (х t + 1, y t + 1 ). Далее путем жеребьевки выбиралось новое преобразование, которое применялось к предыдущей точке для определения координат новой точки, и т. д.