Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

Обратите внимание, что в эксперименте, результатом которого является треугольник Серпинского, а и d всегда равны 0,5, b и с — 0. Значения е и f изменяются для каждого преобразования. Другие природные фракталы, например листья растений, ветки папоротника и т. д., можно получить, рассмотрев различные значения а, Ь, с, d, е и f .

Описанная процедура, названная системой итерируемых функций, представляет собой один из наиболее интересных методов построения фракталов на компьютере. Эксперимент привел к удивительному результату: многие биологические формы и структуры являются фракталами. Если, к примеру, мы применим преобразования (повороты, переносы, изменение масштаба) к точкам, представляющим клетки, то получим структуру, которая будет фракталом, изображающим, к примеру, лист растения.

Одна из классических научных задач — наблюдение за природой и проведение экспериментов. Наблюдение явления подразумевает сбор каких-либо данных. В качестве примера приведем изучение загрязнения окружающей среды, в котором как индикаторы используются некоторые виды лишайников, количество мутаций определенной бактерии или вес мышей из одного помета. На этом этапе исследования ученый подсчитывает, например, количество муравьев, проходящих через определенное место за минуту, или число красных кровяных телец. Вместо подсчетов в некоторых случаях могут требоваться измерения, например кислотности среды, веса, роста или любых других показателей, значение которых, по определению измерения, будет содержать несколько десятичных знаков.

Данные, собранные в ходе эксперимента, объединяются в таблицы. Допустим, что в оранжерее на четырех грядках растет по семь растений, при этом на каждую грядку вносится свое удобрение. Чтобы выяснить, дает ли оно положительный эффект, по прошествии определенного времени производится подсчет числа листьев на каждом растении. Обозначим это число через х . Подобные данные обычно представлены в виде таблиц.

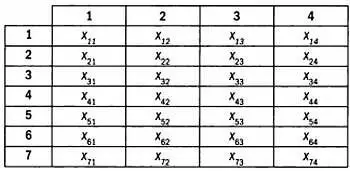
К примеру, х 23будет обозначать число листьев растения 2 с удобрением 3, х 74— число листьев растения 7 с удобрением 4. Математики проводили подобные эксперименты с древних времен, используя так называемые латинские квадраты, то есть таблицы или матрицы, в которых символ (число или сочетание нескольких символов) встречается в каждой строке и каждом столбце только один раз. Разновидностью латинского квадрата является популярная сегодня игра судоку.

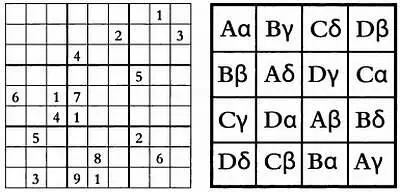
Слева — пример популярной японской головоломки судоку, справа — латинский квадрат.

Теперь предположим, что мы хотим дать общее определение таблице, использованной в эксперименте с растениями и удобрениями. Можно сказать, что даны m растений и n видов удобрений, и записать представленную выше таблицу в круглых скобках:

Такая форма представления данных называется матрицей. Таким образом, матрица размера m х n — это всего лишь множество из m х n элементов, записанных в m строк и n столбцов. Матрицы обычно обозначаются заглавными буквами — А, В, С и т. д. Они позволяют удобно представлять не только данные, но и системы уравнений. Рассмотрим в качестве примера следующую систему линейных уравнений:

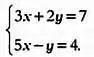
В матричном виде эту систему уравнений можно представить так:

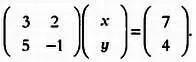
С помощью матриц можно проанализировать также химическую структуру молекулы. К примеру, если мы присвоим произвольные обозначения атомам углерода С в молекуле витамина А , или ретинола, как показано на рисунке

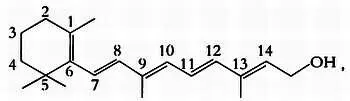
то молекула витамина А будет представлена следующей матрицей.

Обратите внимание, что х ij = 1, если между атомами i и j существует связь, если же связь между атомами отсутствует, х ij = 0.

* * *

ПРЕЛЕСТЬ МАТРИЦ — В ИХ РАЗНООБРАЗИИ

Всевозможные обозначения, связанные с матрицами, встречаются очень часто. Разъясним некоторые популярные термины.

Квадратная матрица — это матрица, в которой число строк и столбцов одинаково:

Симметричная матрица — это квадратная матрица, в которой выполняется соотношение х ij= х ji:

Единичная матрица — это квадратная матрица, все элементы которой равны 0, и только элементы главной диагонали равны 1. Единичная матрица обозначается буквой Е.

Диагональная матрица — это квадратная матрица, все элементы которой равны 0, за исключением элементов главной диагонали:

Нулевая матрица — матрица (необязательно квадратная), все элементы которой равны 0:

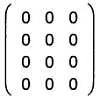
Треугольная матрица — это квадратная матрица, в которой все элементы, расположенные над главной диагональю или под ней, равны 0. Слева представлен пример верхнетреугольной матрицы, справа — нижнетреугольной.

* * *

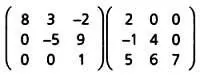
Соотношение между элементами представимо с помощью графа. К примеру, элементы нейронной сети или клеточного метаболизма могут быть представлены узлами, связанными между собой дугами. Таким образом, можно сопоставить матрицу графу, как мы показали в примере с витамином А .