Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

С помощью матрицы можно представить экспериментальные данные, системы уравнений и графы. И по-настоящему важно, что над матрицами мы можем выполнять различные действия. С середины XIX века известны правила операций над «данными, расположенными в строках и столбцах», к примеру, сложение и умножение матриц. С того времени была создана матричная алгебра, составляющая основу многих количественных методов математической биологии и других дисциплин. К примеру, изучение динамических систем в экологии или физиологии, анализ и решение многочисленных задач генетики, как правило, проводятся с помощью операций над матрицами.

В этом разделе мы опишем некоторые наиболее частые операции над матрицами, знание которых поможет понять многочисленные способы применения матриц.

Сложение

Это одна из простейших операций над матрицами. Допустим, в эксперименте рассматриваются две матрицы размером 2 x 2, которые мы обозначим А и В :

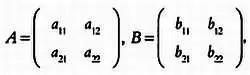
такие, что

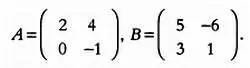
Как будет выглядеть матрица С , равная их сумме, то есть А + В ? Матрица С образуется последовательным сложением элементов исходных матриц: с 11 = а 11 + Ь 11, с 12 = а 12 + Ь 12, с 21 = а 21 + Ь 21 и с 22 = а 22 + Ь 22:

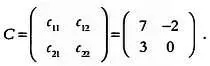
Сложение матриц возможно в том случае, если они имеют одинаковый размер. Предположим, что в лаборатории при изучении детородной функции человека используется модель, в которой яйцеклетка или сперматозоид, несущие доминантный ген A , обозначены 1, рецессивный ген а — 0. Если сперматозоид оплодотворяет яйцеклетку, то все возможные эмбрионы для рассматриваемого гена будет описывать следующая сумма матриц:

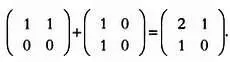
В этом примере 2, 1 и 0 соответствуют эмбрионам с генами АА, Аа и аа соответственно.

Вычитание

Разность матриц А — В определяется как сумма A + (—1)В. Чтобы найти разность матриц А и В из первого примера:

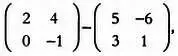
сначала нужно сменить знак элементов матрицы В :

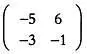
и сложить полученную матрицу с А . Результат будет искомой разностью:

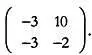
Умножение

Еще одна простейшая операция над матрицами — это умножение матрицы на число. Пусть k — произвольное число, к примеру константа или даже функция у( х ) (математики называют подобные величины скалярными), А — матрица.

Произведение k · А :

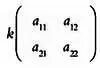
равно

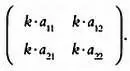
Допустим, что на земельном участке со сниженной плодородностью почвы испытываются четыре удобрения с разным соотношением азота, фосфора и калия. После внесения удобрений на четыре разных участка уровень всхожести семян на первом участке составил 5 %, на втором — 15 %, на третьем — 8 %, на четвертом — 27 %.

Пусть на каждом участке посеяно 80 семян. Обозначим всхожесть на первом, втором, третьем и четвертом участках через а 11, а 12, а 21 и а 22 Число семян, взошедших на каждом участке, будет равно:

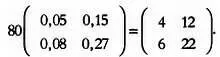
Умножение матриц очень часто используется в математической биологии и других дисциплинах. Чтобы матрицы А и В можно было умножить друг на друга, число столбцов n матрицы А должно быть равно числу строк n матрицы В . Произведением матриц А и В будет матрица С , имеющая m строк и р столбцов. Будем использовать обозначения, которые обычно применяются в математической литературе, и проиллюстрируем операцию умножения матриц.

Пусть даны две матрицы А и В :

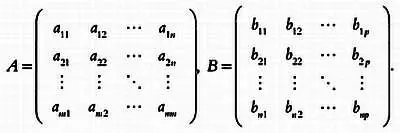
Их произведением будет матрица С :

Элемент с ij матрицы С в общем виде задается следующим выражением:

а i1b 1j = а i2b 2j +… + а inb nj

Таким образом, чтобы вычислить элемент с, нужно взять элементы а 11, а 12 …, Ь 11, b 21 … и найти значение выражения а 11Ь 11 + а 12Ь 21 + … + а 1nЬ n1 .

Проще всего продемонстрировать вычисление произведения матриц на примере

Пусть даны матрицы А и В :

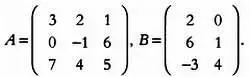
Найдем их произведение A · В , выполнив следующие действия:

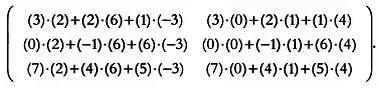
Получим матрицу:

Важно учесть, что сумма матриц А + В не изменится, если мы поменяем слагаемые местами (следовательно, операция сложения матриц является коммутативной), в то время как произведение матриц не обладает этим свойством: произведение матриц A · В не равно произведению В · А . С учетом этого одним из самых интересных действий является умножение матрицы А на матрицу В , состоящую из одного столбца, то есть умножение А m x n · В n x 1 . Матрица, состоящая из одного столбца, называется вектор-столбцом.

Чтобы показать, как применяется произведение матрицы на вектор, представим, что нейробиолог составляет модель нейронной сети. В этой сети группа нейронов (обозначены кругами), которые мы будем называть афферентными, или чувствительными, получает импульсы из внешнего мира, к примеру посредством органов чувств. Афферентные нейроны отправляют сигналы другим нейронам, которые называются эфферентными, или двигательными, через соединения, или синапсы. Задача эфферентных нейронов — отправить ответ на некоторый входной сигнал, поступивший к афферентным нейронам. Этот ответ поступает к мышцам, железам и т. д. Обозначим входной сигнал, поступающий к афферентным нейронам, вектором u ->. Элементами вектор-столбца х 1, х 2 , …, х i . будут, к примеру, характеристики некоторого объекта. Обозначим через y 1 , y 2 , …, y i . составляющие вектора v -> , который будет обозначать ответ эфферентных нейронов после обработки входного сигнала.