Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

Умножим общее число горошин, 660, на вектор-столбец, описывающий второй закон Менделя:

Получим вектор-столбец:

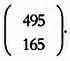
Таким образом, мы должны были получить 495 желтых горошин и 165 зеленых.

Опишем метод, с помощью которого генетики проверяют, соответствуют ли результаты эксперимента математическому закону, а мы сможем узнать, соответствуют ли наши результаты второму закону Менделя.

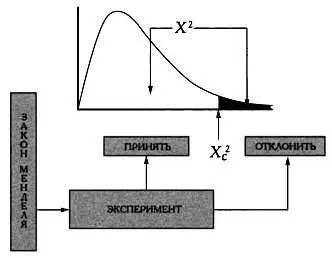
Схема экспериментального метода применительно к менделевским законам наследования — столпам математической биологии.

Для этого мы используем один из самых популярных в биологии статистических критериев — критерий согласия хи-квадрат. Не вдаваясь в детали, вычислим сумму следующих выражений, которая позволит оценить отклонение фактических данных от результатов, на 100 % соответствующих второму закону Менделя. Обозначим отклонение греческой букво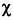й (хи):

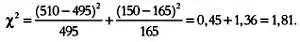
Затем сравним эту сумму с эталонным значением, которое назовем критическим значением хи-квадрат и обозначим c 2Значение c 2для экспериментов Менделя составляет 3,84. Применим следующий критерий: если сумма 2больше, чем c 2, наши результаты не соответствуют второму закону Менделя. Если же сумма 2меньше, чем c 2, экспериментальные результаты соответствуют второму закону Менделя.

Так как 1,81 меньше критического значения 3,84, результаты эксперимента соответствуют этому закону, а отклонение между фактическими значениями (510 и 150) и теоретическими (495 и 165) обусловлено случайными факторами, не имеющими значения для эксперимента.

Является ли наследование признаков независимым?

Напомним, что, согласно второму закону Менделя, признаки А или а передаются независимо друг от друга. Далее Мендель сделал еще один шаг и задался вопросом: если индивид обладает двумя признаками одновременно, как они передаются следующему поколению? Является ли наследование признаков независимым?

Чтобы ответить на этот вопрос, Мендель рассмотрел следующие два признака горошин: гладкая ( А ) или морщинистая ( а ) поверхность и желтый ( В ) или зеленый цвет ( Ь ). После того как Мендель выбрал два анализируемых признака, он скрестил растения двух чистых линий. Горошины растений первой линии были гладкими и желтыми ( ААВВ ), горошины растений второй линии были морщинистыми и зелеными ( ааЬЬ ). Растения, полученные в результате скрещивания, представляли поколение Р , и от их признаков напрямую зависели признаки первого поколения потомков F 1 . Обратите внимание, что все гаметы растений ААВВ имели тип АВ , все гаметы растений ааЬЬ — тип ab . После перекрестного опыления растений из различных линий все растения в поколении Fx имели гладкие желтые горошины (генотип АаВЬ). Получив этот результат, Мендель задался вопросом: какими должны быть потомки растений с генотипом АаВЬ , принадлежащих к поколению F 1 , или каким будет генотип растений поколения F 2 ? В итоге Мендель сформулировал третий закон, или закон независимого наследования признаков.

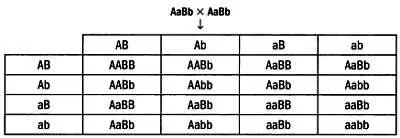
Третий закон Менделя.

В самом деле, 16 растений поколения F 2 были получены путем комбинирования четырех классов гамет растений АаВЬ , то есть АВ, аВ, АЬ и ab , на решетке Пеннета, которая крайне полезна при определении потомства из поколения F 2 согласно третьему закону Менделя.

Обратите внимание, что 16 полученных генотипов можно разделить на следующие группы:

• 9 горошин — желтые гладкие ( АхВу );

• 3 горошины — желтые морщинистые (а аВу );

• 3 горошины — зеленые гладкие ( АхЬЬ );

• 1 горошина — зеленая морщинистая ( aabb ).

При этом х может иметь значение А или а, у — В или Ь . Если мы представим этот закон наследования в матричном виде, получим:

В заключение этого раздела опишем еще один похожий эксперимент. На этот раз по результатам эксперимента было получено 1425 горошин: 807 — желтые гладкие ( АхВу ), 270 — желтые морщинистые ( ааВу ), 265 — зеленые гладкие ( Axbb ), 93 — зеленые морщинистые ( aabb ). Соответствуют ли эти результаты третьему закону Менделя? Чтобы убедиться в этом, вначале нужно определить эталонные значения:

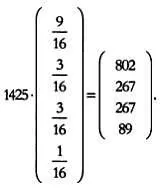
Затем нужно оценить, насколько велико отклонение между эталонными значениями и результатами эксперимента. Для этого вновь применим критерий согласия хи-квадрат. Дальнейшие расчеты оставляем заинтересованному читателю.

* * *

МЕНДЕЛЬ И ЗАКОНЫ НАСЛЕДОВАНИЯ

Ботаник Грегор Мендель родился в Австрии в 1822 году. В 1843 году он постригся в монахи августинского монастыря в Брюнне (ныне Брно, Чехия). В своем маленьком саду размерами всего 35 на 7 метров Мендель в 1857 году начал эксперименты по перекрестному опылению гороха, а позднее на основании своих экспериментов сформулировал знаменитые законы наследования признаков.

Гениальность Менделя проявилась в том, что он изучил всего несколько признаков гороха ( Pisum sativum ) и рассматривал их по отдельности. Кроме того, ботаник различал доминантные признаки, которые обозначал заглавными буквами ( A, В, С…) и рецессивные (их он обозначал строчными буквами а, б, с, …) При исследовании он сосредоточился на форме горошин (гладкие Аили морщинистые а), их цвете (желтый Вили зеленый Ь) и некоторых других признаках — положении цветка, форме и цвете стручков и т. д. Одним из залогов успеха Менделя стало использование так называемых чистых линий ( АA, аа) и отсутствие самоопыления во время экспериментов.

Основной вывод исследователя заключался в том, что наследование признаков можно описать простыми математическими законами. Он отправил полученные результаты знаменитому швейцарскому ученому Карлу Вильгельму фон Негели, однако тот проигнорировал письмо. Мендель опубликовал свою работу под названием «Опыты над растительными гибридами» ( Versuche liber Pflanzenhybriden ) и в 1865 году представил ее в Обществе естествоиспытателей в Брно, но его труд вновь остался без внимания. По-видимому, Мендель писал о полученных результатах и Дарвину, но тот также не прочел его послание. 35 лет труды ботаника оставались незамеченными. Умер Мендель в 1884 году, а его работы были повторно открыты лишь около 1900 года.