Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

( u 1u 2 … u m ).

Далее вы узнаете, как векторы используются в изучении локомоции (перемещения животных) и при анализе нейронных сетей.

Один из самых интересных способов применения векторов — изучение локомоции животных. Кузнечики прыгают, люди могут поднимать тяжести руками, рыбы плавают, птицы летают. Понять механику этих движений помогают операции с векторами.

Если мы рассмотрим движение руки человека, один вектор можно будет сопоставить бицепсу (этот вектор будет обозначать силу сокращения мышц), второй вектор будет обозначать противодействующую силу, третий вектор — указывать вес объекта, который поднимает рука.

Сложение векторов также помогает понять функцию некоторых мускулов. Один из методов сложения векторов — это известное правило параллелограмма. Заключается оно в том, что нужно привести два вектора, сумму которых мы хотим найти, к общему началу. Затем на этих двух векторах нужно построить параллелограмм.

К примеру, если рассмотреть ногу человека и обозначить боковую часть четырехглавой мышцы бедра вектором F L -> , а среднюю часть этой мышцы — вектором F M -> , сумму этих векторов можно найти по правилу параллелограмма. Иными словами, сумма векторов F L -> + F M -> будет обозначать суммарную силу четырехглавой мышцы F -> .

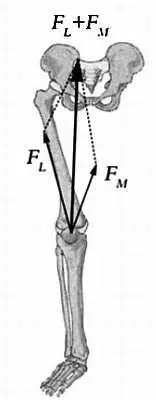
Сумма векторов, соответствующих мышцам ноги, найденная по правилу параллелограмма.

Другой классический пример — сила F -> , с которой сокращаются мышцы-сгибатели предплечья. Если представить эту силу в виде вектора, то она будет равна сумме двух других векторов, соответствующих другим мышцам. Один из этих векторов, F U -> , перпендикулярен предплечью, второй вектор, F И -> , параллелен предплечью.

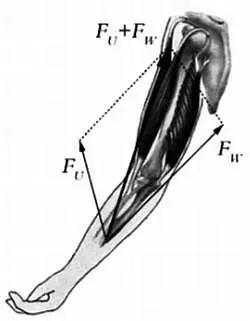
Сумма векторов, соответствующих мышцам руки, найденная по правилу параллелограмма.

Если векторов больше двух, их сумму можно найти по правилу многоугольника. Заключается оно в том, что конец каждого вектора совмещается с началом следующего. Суммой исходных векторов будет вектор, начало которого совпадает с началом первого вектора, конец — с концом последнего вектора. Этот метод полезен при вычислении скорости движения корабля, полета птиц, перемещения пловца или рыбы.

В примерах с птицей или рыбой результирующая скорость будет равна сумме всего двух векторов. Но в силу особенностей задачи для сложения векторов используется не правило параллелограмма, а правило многоугольника.

Допустим, что рыба или птица движется в воде или в воздухе со скоростью, обозначаемой вектором V A ->, V M -> — скорость течения воды (или ветра). Как следствие, вектор результирующей скорости V -> будет равен сумме векторов V A -> и V M -> , определяемой по правилу многоугольника.

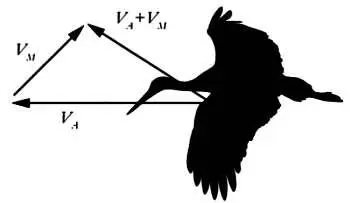
Сумма векторов в примере с полетом птицы, найденная по правилу многоугольника.

Достаточно помнить, что во всех подобных примерах, если вы хотите найти результат как вектор-столбец, к примеру F ->, V -> :

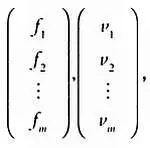
нужно сложить векторы по тому же правилу, что и матрицы, то есть F U -> + F И ->, F L -> + F M -> и V A -> + V M -> соответственно.

Помимо сложения, существует множество способов применения других операций над векторами. Так, умножение векторов успешно используется в математических моделях, описывающих наиболее характерные функции мозга.

Когда мы говорили об операциях над матрицами, мы представили модель нейронной сети, основанную на произведении вектора и матрицы:

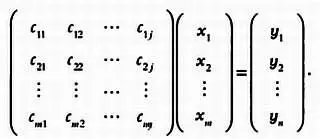
Нейронную сеть также можно представить в более простом виде:

M · u -> = v -> .

В соответствии с вышесказанным, u -> — вектор, представляющий слой входных, или афферентных, нейронов, вектор v -> — слой выходных, или эфферентных нейронов.

М — матрица связей между нейронами этих двух слоев, также известная как матрица памяти. Это название указывает на то, что именно в связях между нейронами, синапсах, мозг хранит всю известную нам информацию.

Эту гипотезу выдвинул испанский исследователь Сантьяго Рамон-и-Кахаль, а позднее развил американский ученый Дональд Хебб. В настоящее время нейробиологи считают, что именно в связях между нейронами фиксируются черты лиц знакомых нам людей, очертания букв, чисел и многие другие образы.

Сантьяго Рамон-и-Кахаль(1852–1934) в лаборатории. Справа изображен один из его рисунков, описывающих нейронные сети.

Следовательно, если мы рассмотрим произвольную строку матрицы М как вектор-строку, описывающий связи между определенным выходным нейроном и всеми входными нейронами, то состояние этого выходного нейрона можно будет вычислить так, как мы объясняли в прошлой главе. Операция над векторами называется скалярным произведением. Рассмотрим два вектора: вектор-строку а -> (исключительно из формальных соображений дополним это обозначение буквой t , что означает «транспонированный») и вектор-столбец Ь -> . Скалярное произведение этих двух векторов будет равно:

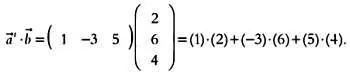
Выполнив указанные арифметические действия, получим итоговый результат, равный 4. Скалярное произведение, которое также называют внутренним произведением векторов, — это число, указывающее длину проекции вектора-строки а -> на вектор Ь -> . Если известны длины обоих векторов, | а -> | и | Ь -> |, а также угол α между ними, то скалярное произведение векторов а -> · Ь -> будет равно | а -> |·| Ь -> |·cos α . Этот результат представляет для нас особый интерес, если учесть, что | а -> |·cos α — это значение проекции вектора а -> на вектор Ь -> .

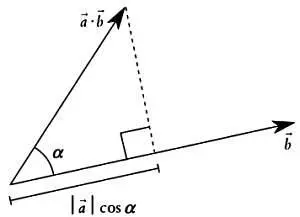
Скалярное произведение векторов а -> · Ь ->