Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

С учетом того, что а 13 имеет знак +, получим:

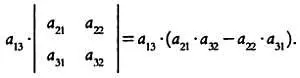
Теперь, чтобы вычислить определитель матрицы А , нужно свести полученные выше результаты в одно выражение:

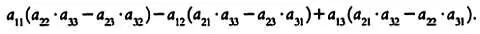
Пусть дана матрица A :

Ее определитель вычисляется следующим образом:

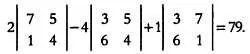
Предположим, что даны три вектора, исходящие из одной точки. Допустим, их координаты таковы: u -> = (2, -1, 4), v -> = (3, 3, -2) и w -> = (-3, 2, 1). Если мы вычислим определитель:

получим 71. Что означает это число? Поскольку в нашем примере векторы исходят из одной точки, значение определителя равно объему параллелепипеда, построенного на этих трех векторах.

Любопытно, что деление матрицы на матрицу невозможно. Однако на помощь придет математическая смекалка. Допустим, что мы хотим разделить 5 на 2, то есть найти значение 5/2, при этом использовать операцию деления нельзя. Напомним, что:

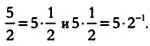
Следовательно, если мы заменим числа 5 и 2 матрицами А и В , получим:

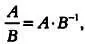
где В -1— матрица, обратная В . Обратите внимание, что произведение В · В -1будет равно единичной матрице Е . Отметим, что матрица В должна быть квадратной, то есть иметь одинаковое число строк и столбцов. Кроме этого, матрица В будет иметь обратную только в том случае, если ее определитель отличен от 0.

Найти обратную матрицу для матрицы 3 x 3 несложно, хотя для этого потребуются трудоемкие вычисления. Читатель легко найдет всю интересующую информацию по этому вопросу самостоятельно. Обратную матрицу для матрицы 2 x 2 очень просто найти следующим способом. Пусть дана матрица А :

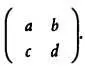
Обратная ей матрица А -1определяется напрямую. Она имеет вид:

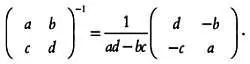
Напомним, что 1/( ad — bc ) — величина, обратная определителю матрицы. Применив программу символьных вычислений Derive , найдем матрицу, обратную матрице А (не будем приводить все промежуточные действия):

Если мы запишем в программе выражение: А ^(—1), то получим А -1то есть обратную матрицу:

Обратные матрицы часто используются в трехмерном компьютерном моделировании, а умножение матриц полезно для обсчета поворотов, например при компьютерном моделировании поворота головы динозавра. Подобные модели широко применяются в биомедицине, а обратные матрицы — при шифровании сообщений, а также в некоторых основных статистических методах многовариантного анализа, который представляет собой совокупность статистических методов, применяющихся для анализа данных в биологии и медицине. Также операции над матрицами используются для решения систем линейных уравнений, о чем мы расскажем в следующей главе.

С исторической точки зрения законы Менделя, сыгравшие важную роль в зарождении генетики, не только знаменуют одну из важнейших вех в биологии, но и представляют собой прекрасный пример полных факторных экспериментов. В этом разделе мы представим элементарную модель знаменитых законов наследования, в которой используются матрицы.

Первый закон Менделя, или закон единообразия гибридов ( Аа ) первого поколения F 1 , был выведен экспериментально следующим образом. Представьте, что мы скрестили два растения, относящихся к разным чистым линиям ( АА и аа ). У растения АА все горошины желтые, у растения аа — зеленые. Скрещивание выполняется методом перекрестного опыления: мы отрезаем ножницами тычинку одного растения, например аа, чтобы избежать самоопыления. Затем мы собираем пинцетом пыльцу с другого растения, АA , и переносим ее на первое растение, аа . Изучив потомство, которое Мендель называл первым поколением, или F 1 , можно убедиться, что все горошины имеют желтый цвет и принадлежат к гибридному типу Аа .

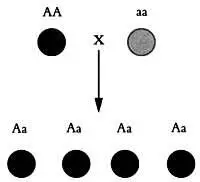
Первый закон Менделя.

После экспериментов, которые помогли Менделю сформулировать первый закон наследования, ученый захотел узнать, отличаются ли желтые горошины ( F 1 ), полученные в ходе эксперимента, от горошин растений чистой линии ( АА ). Чтобы найти ответ на этот вопрос, Мендель провел самоопыление растений из поколения F 1 и изучил их потомство, рассмотрев в общей сложности 8023 горошины. После тщательного подсчета ученый обнаружил, что 3/4 горошин были желтыми, 1/4 — зелеными. Этот результат привел к открытию второго закона наследования, или закона расщепления признаков во втором поколении.

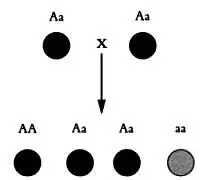
Второй закон Менделя.

В матричном представлении второй закон Менделя выглядит так:

Обратите внимание, что этот вектор отражает соотношения, которые генетики называют расщеплением по фенотипу. Сумма элементов матрицы (которая в этом случае состоит из одного столбца) равна единице. В биологической математике такая матрица называется стохастической.

Представьте, что мы провели эксперимент и получили 660 горошин, 510 из них оказались желтыми, 150 — зелеными. Соответствуют ли эти результаты второму закону Менделя? Чтобы узнать это, необходимо ответить на вопрос: каким должно быть количество желтых и зеленых горошин в точном соответствии с этим законом?