Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

* * *

Одна из самых перспективных областей биоинформатики, дающая ответ на вопрос об эволюции видов, — это изучение генома отдельных видов, то есть совокупности генетической информации, записанной в ДНК его клеток. Для анализа генома используются матрицы, элементами которых являются вероятности. Отметим, что вероятность — это величина, характеризующая частоту, с которой наблюдается определенный результат или исход того или иного события. Вероятность — число, заключенное в интервале от 0 до 1. Если результат эксперимента невозможен, говорят, что его вероятность равна 0. Если результат эксперимента наблюдается всегда, его вероятность равна 1. К примеру, при броске кубика вероятность получения любого результата {1, 2, 3, 4, 5, 6} равна 1/6. Вероятность того, что выпадет четное число очков {2, 4, 6}, равна 1/2.

Одна из особенностей подобных экспериментов заключается в том, что кубик или монета не имеют памяти, то есть исход эксперимента не зависит от предыдущих результатов. Математик Андрей Марков изучил последовательности случайных событий, обладающие памятью, которые получили название цепей Маркова. В них вероятность того или иного исхода зависит от предыдущих результатов. Таким образом, цепи Маркова описывают эксперименты или явления, в которых последний результат влияет на последующие. К примеру, вероятность того, что в определенный момент в будущем, t + 1, определенный участок цепочки ДНК будет содержать то или иное азотистое основание {А, Т, Г, Ц} (аденин, тимин, гуанин или цитозин), зависит от того, какое основание занимало этот участок цепочки ДНК в момент времени t . Если учесть все возможные перестановки или мутации определенного азотистого основания ДНК, получится следующая матрица:

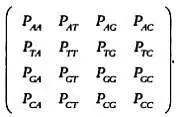
В соответствии с этой матрицей для некой молекулы ДНК вероятность того, что в определенном участке цепочки аденин А сменится цитозином Ц , равна Р АЦ .

Цепи Маркова используются при изучении структуры белков, для прогнозирования областей генома, которыми кодируются белки, а также при изучении эволюции видов путем анализа цепочек ДНК.

В повседневной жизни мы довольно часто измеряем значения величин, к примеру, температуру в комнате или вес пакета кофе. В науке измерения также имеют большое значение. Химики в лаборатории измеряют кислотность вещества, определяя показатель pH, а биологи оценивают парциальное давление O 2. Особенность этих измерений состоит в том, что значение величин не зависит от направления измерения.

Так, температура окружающей среды не зависит от того, где именно мы поместим термометр, при измерении pH вещество считается достаточно однородным, поэтому местоположение электрода также не влияет на результат. Такие величины, значение которых выражается одним числом, называются скалярными.

Однако существует множество ситуаций, когда направление измерения так же важно, как и значение величины. К примеру, в физике скорость, ускорение, сила и электрическое поле характеризуются не только числом, но и направлением. Механизмы сокращения мышц позвоночных устроены так, что мышца сокращается только в определенном направлении. Подобные величины, которые характеризуются не только числом, но и направлением, называются векторными.

Как следует из названия, для представления векторных величин используются математические объекты, называемые векторами. Вектор имеет численное значение — модуль, который соответствует его длине и равен значению величины, изображаемой вектором (к примеру, скорости). Также вектор имеет направление.

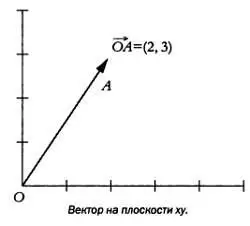
Но какое отношение векторы имеют к матрицам? Действия над матрицами — один из способов выполнения операций над векторными величинами, которые, как нетрудно убедиться, широко применяются не только в науке и технике, но и в повседневной жизни.

Так, матрица с произвольным числом строк m и единственным столбцом обозначает вектор и называется вектор-столбцом. Векторы обозначаются u ->, v -> и т. д. К примеру, вектор u ->записывается так:

Логично предположить, что число элементов вектора, m , имеет отношение к важному его свойству — оно соответствует размерности пространства, в котором мы работаем. В частности, вектор

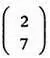
соответствует векторной величине на плоскости. Начало этого вектора находится в точке (0, 0), конец — в точке (2, 7). Следующий вектор расположен в пространстве (очевидно трехмерном):

Начало этого вектора находится в точке (0, 0, 0), конец — в точке с координатами (3,1,3).

Чему равно значение величины, изображаемой этим вектором? Если обозначить рассматриваемый вектор через u ->, достаточно будет вычислить:

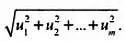
В математике модуль вектора обозначается | u |. К примеру, модули двух описанных выше векторов равны:

* * *

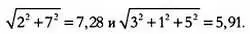
ВЕКТОРНОЕ ПРОСТРАНСТВО

В результате изучения матриц и систем линейных уравнений в XVII веке было определено понятие векторного пространства. Не будем останавливаться на нем подробнее, отметим лишь, что с точки зрения математики возможность сложения векторов (то есть выполнения операции u ->+ v ->) и умножения произвольного числа kна вектор u ->( k· u ->) вкупе с соблюдением некоторых свойств позволяет определить векторное пространство как множество векторов, обладающее определенными характеристиками. Векторное пространство является одним из основных понятий в математической биологии. Оно используется в изучении филогенеза, при классификации цепочек ДНК, в экологических моделях, при исследовании метаболизма или восприятия цветов, а также в других областях.

* * *

Если возникает необходимость определить вектор-строку, достаточно применить операцию транспонирования: