Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

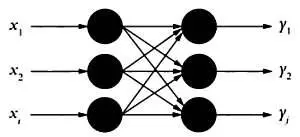
Модель нейронной сети.

Наконец, представим синапсы между афферентными и эфферентными нейронами в виде матрицы М. Назовем ее матрицей памяти. Каждый элемент с этой матрицы обозначает связь между входным, или афферентным, нейроном i и выходным, или эфферентным, нейроном j . Учитывая вышесказанное, модель нейронной сети можно сформулировать с помощью матричной алгебры. Имеем:

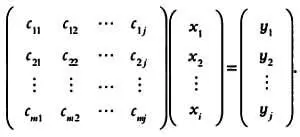
Если нейробиолог, используя эту модель, захочет узнать ответ эфферентного нейрона № 2, зная все остальные значения, ему достаточно будет вычислить:

y 2 = С 21Х 1 + С 22Х 2 + … + C 2jX i

А если нужно определить выходное значение для первого эфферентного нейрона?

В этом случае достаточно вычислить y 1 = С 11Х 1 + С 12Х 2 + … + C 1jX i

Пусть дана нейронная сеть с тремя входными, или афферентными нейронами, и тремя выходными, или эфферентными нейронами. Матрица связей, или синапсов, между нейронами М приведена ниже:

Если к слою входных нейронов поступает извне следующий сигнал:

каким будет выходное значение для первого эфферентного нейрона? В соответствии с описанной моделью имеем:

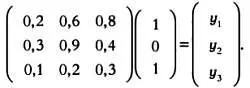
Искомое выходное значение равно у 1 = 0,2·1 + 0,6·0 + 0,8·1, и, как следствие, у 1 = 1.

Сегодня этот класс математических моделей используется для распознавания образов — букв, чисел, фотографий и т. д. в системах искусственного интеллекта.

Транспонирование матриц

Еще одна привычная операция над матрицами называется транспонированием. Для того чтобы получить транспонированную матрицу А' для матрицы А , достаточно поменять строки исходной матрицы на столбцы. Пусть дана матрица А :

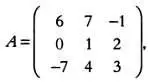
транспонированная матрица А' будет выглядеть так:

Транспонированная матрица определяется мгновенно. В самом деле, если мы транспонируем транспонированную матрицу, то есть найдем ( А t ) t , то вновь получим матрицу А . Покажем, где применяется эта операция.

Предположим, что ученый работает с моделью, в которой определена квадратная матрица, то есть матрица с равным числом строк и столбцов. В этом случае существует особое число, соответствующее матрице, которое указывает на некоторые ее любопытные свойства. Это число называется определителем матрицы. Рассмотрим простейший случай — матрицу 2 x 2 (две строки и два столбца), элементы которой обозначим через а, Ь, с и d :

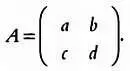
Определитель матрицы А будет равен:

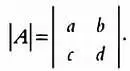
Значение определителя будет равно а · d — b · с . Иными словами, нужно найти произведение элементов на главной диагонали и вычесть из него произведение элементов на побочной диагонали. Определитель матрицы А будет равен 2, так как:

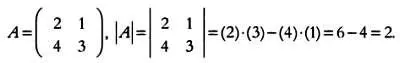
Швейцарский математик Габриэль Крамер(1704–1752) сформулировал правило, носящее его имя, которое позволяет решать системы линейных уравнений с помощью определителей.

Отметим, что мы заменили круглые скобки, типичные для матрицы, двумя прямыми линиями — именно так обозначаются определители. Любопытно, что определители были созданы раньше, чем матрицы, и были известны в Древнем Китае за 300 лет до Рождества Христова. Древние китайцы использовали понятие, схожее с понятием определителя, располагая неизвестные системы линейных уравнений на шахматной доске. Европейские математики впервые применили определители для решения систем линейных уравнений лишь в 1750 году (это сделал Габриэль Крамер). В XIX веке с определителями работали другие математики, в частности Коши. Матрицы появились позднее, так как нужно было дать какое-то название объекту, для которого рассчитывались определители.

Определитель квадратной матрицы размером 3 x 3

Мы уже показали, как вычислить определитель второго порядка. Сделаем еще один шаг вперед. Пусть дана квадратная матрица третьего порядка:

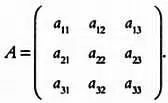
Будем считать, что каждому ее элементу соответствует знак + или —, как если бы речь шла о кристалле хлорида натрия, то есть обычной поваренной соли:

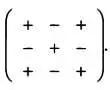
Выберем, к примеру, первую строку матрицы и исключим ее из рассмотрения. Затем исключим элементы первого столбца матрицы:

Выполним над элементами матрицы следующие операции:

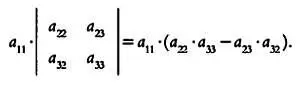
Обратите внимание, что а 11 положительно, так как этому элементу матрицы соответствует знак +.

После того как мы исключили из рассмотрения первую строку и первый столбец матрицы, оставшиеся элементы образуют новую матрицу. Определитель полученной матрицы называется минором М ij , где i и j — номер строки и столбца, исключенных из рассмотрения. В нашем примере i = 1, j = 1.

Выполним аналогичные действия для второго столбца матрицы:

Учитывая, что элемент а 12 имеет знак —, получим:

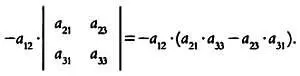
Повторим аналогичные действия для третьего столбца: