Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

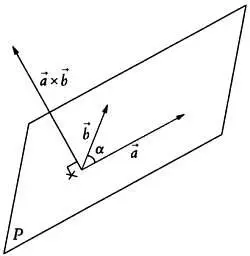
Векторное произведение векторов а ->х Ь ->

Модуль нового вектора c -> будет схож со скалярным произведением, однако его значение будет равно | а -> |·| Ь -> |·sin α . Модуль векторного произведения векторов будет равен площади построенного на них параллелограмма. Направление вектора c -> определяется по известному правилу буравчика, или правилу правой руки.

В биологии векторное произведение используется при изучении молекул, играющих основную роль в поддержании жизни, к примеру таких белков, как миоглобин. Сюда же относится самая знаменитая из всех известных сегодня молекул — молекула ДНК. При их изучении биофизики используют классические понятия физики и измеряют величины, рассчитываемые как векторное произведение, к примеру дипольный момент — электромагнитную силу, действующую на частицу в магнитном поле.

Существует еще одна поистине замечательная операция — тензорное произведение, которое применяется в математических моделях нейронных сетей, описывающих память животных и человека. Представим, что вектор v -> состоит только из единиц и нулей, то есть является двоичным вектором. Каждый из его элементов обозначает наличие (1) или отсутствие (0) той или иной характеристики некоторого объекта.

Если мы вычислим тензорное произведение v -> и v -> , то получим следующую матрицу:

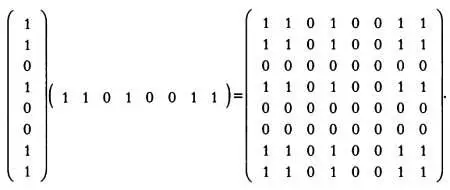
Обратите внимание, какие действия мы выполнили, чтобы получить эту матрицу:

Несмотря на кажущуюся сложность, эта операция на самом деле проста. Мы получили матрицу памяти, обладающую свойством запоминать предмет, показанный нейронной сети. Она позволяет смоделировать на компьютере способность людей и животных запоминать различные объекты. Так как элементы матрицы обозначают связи между нейронами, в модели предполагается, что каждый нейрон связан со всеми другими нейронами. Как следствие, все элементы главной диагонали матрицы должны быть равны 0. Исправим значения элементов главной диагонали, равные 1:

Существуют математические методы, позволяющие восстановить объект, представленный матрицей, и смоделировать процесс вспоминания и распознавания образов.

* * *

СЕТЬ ХОПФИЛДА

Механизм обучения, запоминания букв, цифр и сигналов светофора можно смоделировать с помощью нейронной сети. Модель памяти, определяемая с помощью тензорного произведения, известна как сеть Хопфилда. Она названа в честь исследователя Джона Джозефа Хопфилда, который представил эту модель в 1980-е годы. Сегодня модель Хопфилда используется в самых разных цифровых системах: не только для решения множества физических задач, но и в электронике, и при обработке изображений.

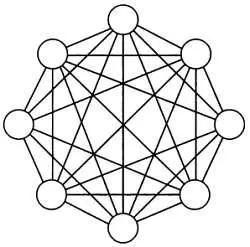
Модель памяти Хопфилдаиз восьми нейронов. Каждый нейрон в этой модели связан со всеми остальными.

* * *

Обратные матрицы применяются также для решения систем уравнений. Рассмотрим систему из трех уравнений с тремя неизвестными:

а 11х + а 12y + а 13z = b 1

а 21х + а 22y + а 23z = b 2

а 31х + а 32y + а 33z = b 3

Матрицы также используются для представления систем уравнений:

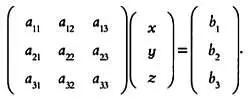
Это равенство равносильно следующему:

А · X = В .

Если мы найдем матрицу, обратную А , то есть А -1 , а затем умножим обе части равенства на эту обратную матрицу:

А -1 ·А·Х = А -1 · В ,

то, поскольку произведение А · А -1 равно единичной матрице Е , имеем:

Е · Х = А -1 · В .

Кроме того, так как произведение любой матрицы на единичную матрицу Е равно исходной матрице, получим:

Х = А - 1· В .

Таким образом, решить систему уравнений, то есть определить значения х, у, z , можно с помощью обратной матрицы коэффициентов: нужно умножить ее на вектор-столбец свободных членов системы уравнений.

Продемонстрируем этот метод на примере под названием «эксперимент энтомолога». Допустим, что мы отправились в поле в поисках определенного вида насекомых и разместили ловушки там, где эти насекомые водятся. Спустя несколько дней мы вернулись к ловушкам, чтобы собрать насекомых. В лаборатории мы установили, что в ловушках оказалось 180 насекомых. Мы разделили их на молодых (обозначим их через х) и взрослых ( у ) особей. Имеем первое уравнение системы:

х + у = 180.

На основе результатов аналогичных экспериментов, проведенных ранее, мы знаем, что для насекомых этого вида соотношение молодых и взрослых особей равно 2 к 1. Кроме того, в силу естественных причин 6 взрослых насекомых умерло:

2 х = у — 6.

Чтобы определить численность молодых и взрослых особей, нужно решить следующую систему уравнений:

х + у = 180,

2 х = у — 6.

Второе уравнение можно записать в виде: 2 х — у = —6. Система примет вид:

х + у = 180,

2 х — у = -6.

В матричной нотации эта система уравнений записывается так:

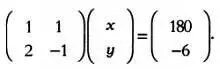
Имеет ли система уравнений решение?

Проницательные математики имеют одну достойную привычку — они не тратят время на бесполезные действия. Одним из наиболее ярких примеров этому является решение систем уравнений. Рассмотрим все возможные группы систем уравнений.

Во-первых, система может не иметь решений — в этом случае она называется несовместной. Представим, что система состоит из двух уравнений, описывающих две параллельные прямые. Поскольку прямые не пересекаются, система не будет иметь решений. Во-вторых, система может иметь бесконечно много решений, то есть быть неопределенной. Продолжив аналогию с прямыми, такая система состоит из двух уравнений, описывающих две совпадающие прямые, имеющие бесконечно много общих точек. Наконец, если система из двух уравнений описывает прямые, пересекающиеся в одной точке, она называется совместной и определенной. Ее решением будет единственная точка пересечения прямых ( х, у ).