Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

dx / dt = — px + qxy

Обратите внимание, что естественная убыль хищников компенсируется ростом их численности при охоте на жертв (именно поэтому qxy имеет знак плюс). Следовательно, хищники не вымрут, имея достаточно пропитания.

Аналогично хищники компенсируют естественный рост численности жертв, поэтому в дифференциальное уравнение включается член — sxy со знаком минус, где s — параметр, описывающий взаимодействие хищников и жертв:

dy / dt = ry — sxy .

Одна из предпосылок моделей Вольтерры и Лотки заключалась в том, что отдельные особи, к примеру волки и зайцы, ведут себя подобно частицам газа. Проведя параллель с так называемым законом действующих масс, мы обнаружим, что число взаимодействий между хищниками и жертвами зависит от столь очевидных параметров, как число хищников х и число жертв у . По этой причине их взаимодействие обозначается произведением этих чисел, то есть х · у с соответствующими коэффициентами: qxy и — sxy .

Объединив два описанных выше дифференциальных уравнения в систему:

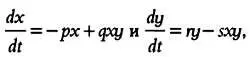
получим знаменитую систему уравнений Лотки — Вольтерры.

После того как мы учли взаимодействие хищников и жертв, решить эту систему уже не так просто, как раньше. В соответствии с моделью, при высокой численности жертв возрастет и число хищников, однако по мере поедания жертв популяция хищников также сократится. В свою очередь, ввиду снижения численности хищников число жертв вновь возрастет, и это вновь приведет к увеличению числа хищников.

Если представить подобные циклические колебания численности популяций на одном графике, мы получим цикл, имеющий название «цикл — решение», так как он является решением уравнений Лотки — Вольтерры.

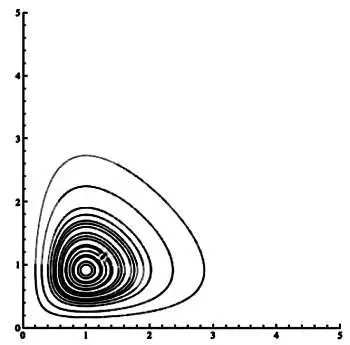
Модель «хищник — жертва» Лотки— Вольтерры: число хищников обозначено на оси у, число жертв — на оси х.

Получить «цикл — решение» системы уравнений можно разными способами, но самым важным из них является рассмотрение колебаний численности популяций. Форма цикла зависит от начального числа хищников и жертв.

Столь же нетрудно найти точку равновесия, так как ее координаты равны:

Нужно очень четко представлять себе описанные колебания системы, особенно когда речь идет о климатических моделях (о них мы поговорим в следующем разделе).

* * *

КОНКУРЕНЦИЯ МЕЖДУ ВИДАМИ

Помимо модели «хищник — жертва», Лотка и Вольтерра представили еще одну модель, описывающую конкуренцию между двумя популяциями или видами. Допустим, что две популяции конкурируют за один и тот же ресурс, при этом рост их численности описывается логистической моделью.

Обозначив через хи учисленность особей в популяциях, имеем:

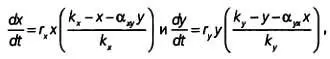
где r x, r у— коэффициенты роста, k x, k y— поддерживающие емкости для каждой популяции. Эти выражения также содержат коэффициенты α, описывающие взаимодействие между особями в популяциях. Иными словами, α xyобозначает воздействие, которое оказывает вид уна вид х, в то время как α yx- это воздействие хна у. Модель можно расширить для нескольких видов, однако это несколько усложнит анализ возможных ситуаций.

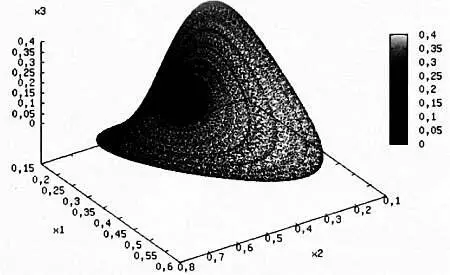
Модель межвидовой конкуренции Лотки— Вольтеррыдля четырех видов.

* * *

В последние десятилетия весьма актуальна тема глобального потепления. Хотя метеорологические центры составляют прогнозы погоды с применением сложных математических моделей, на их основании довольно трудно дать ответ на вопрос, действительно ли наблюдается глобальное изменение климата.

Математические модели, используемые в метеорологии, называются климатическими моделями. Они основаны на описаниях атмосферных процессов и компьютерном моделировании взаимодействия атмосферы и океанов, суши и шапок льда на полюсах. Эти модели представляют собой дифференциальные уравнения, в основе которых лежат законы физики. При их составлении поверхность Земли делится на квадраты, которые описываются уравнениями. Затем вычисляется скорость ветров, относительная влажность воздуха, теплопередача и так далее, а также взаимодействие между соседними областями. На основе интерпретации итоговых результатов моделирования метеорологи и составляют свои прогнозы.

Математические модели атмосферы позволяют предсказывать погоду.

К наиболее надежным метеорологическим данным относятся так называемые климатические режимы, которые учитывают преобладающее направление ветра и другие параметры, описывающие ожидаемую погоду — солнечную, облачную или дождливую. Климатические режимы определяются с помощью статистических методов на основе данных о погоде прошлых лет в стране или регионе. Однако поскольку атмосфера представляет собой хаотическую систему, стоит задуматься, насколько достоверны прогнозы погоды?

Подобные вопросы навели Эдварда Лоренца на мысль изучить атмосферу с точки зрения теории хаоса. Первые попытки составить прогноз погоды были предприняты задолго до 1960-х годов, когда работы Лоренца увидели свет, — это попытались сделать Жюль Чарни, Филип Томпсон, Ларри Гейтс, Рагнар Фьюртофт и гениальный Джон фон Нейман в 1950-х годах с помощью одного из первых компьютеров в истории — ENIAC.

В то время на вычисление прогноза погоды на следующий день требовалось целых 24 часа, а его точность оставляла желать лучшего. Именно в те годы родилась фраза «климат — это то, что ожидается, а погода — то, что будет». В модели, использованной для составления прогноза погоды, атмосфера была представлена решеткой из 270 точек, расположенных на территории Северной Америки и удаленных друг от друга на расстояние 700 километров. Метод конечных разностей позволил решить с помощью ENIAC дифференциальные уравнения, а также уравнение завихренности, которое использовалось в упрощенной модели атмосферы.