Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

А = А s · S + A x · S x + А y · S y ,

где A s — альбедо той части суши, где не растут маргаритки (площадь этой части суши равна S ), А х — альбедо, вызванное белыми маргаритками (площадь суши, где растут белые маргаритки, равна S x ), А y — альбедо, вызванное черными маргаритками (доля земной поверхности, где они произрастают, равна S y ). Обратите внимание, что выражение, по которому рассчитывается альбедо, описывает модель энергетического баланса планеты. Напомним, что черные маргаритки отражают меньше света, чем открытая суша, а белые маргаритки — больше, чем суша. Иными словами, выполняется следующее неравенство: А y < А s < А х .

Цель простейшего эксперимента с моделью «Маргариткового мира» — изучить, как изменяется доля поверхности планеты, где произрастают белые и черные маргаритки. Как правило, в модели используются следующие значения: А y = 0,25, А s = 0,50, А х = 0,75, γ = 0,30. Планета, где в изобилии растут белые маргаритки, будет холоднее, чем планета, изобилующая черными цветами. После увеличения числа белых маргариток, вызванного нагреванием планеты, температура будет снижаться, и напротив, любое снижение температуры на планете будет компенсироваться ростом числа черных маргариток. Кроме того, для некоторых значений параметров возможны два равновесных состояния: планета будет либо совершенно безжизненной, либо полностью покрытой маргаритками.

На страницах этой книги мы совершили увлекательную экскурсию, во время которой показали, что причиной удивительного прогресса биологии и биомедицины во многом стало плодотворное сотрудничество математики и науки о жизни. Использование дифференциальных уравнений, теории хаоса, программ символьных вычислений, операций над векторами и матрицами (и линейной алгебры) позволяет биоматематикам описать красоту и сложность жизни с помощью математических выражений. Благодаря математике ученые могут создавать модели, делать прогнозы относительно самых разных проявлений жизни, будь то гены, белки, клетки, организмы, популяции или экосистемы. Мы надеемся, что после прочтения этой книги читатель захочет подробнее узнать о математической биологии, или биоматематике — науке с богатыми традициями и большими перспективами.

По какой-то странной причине комплексные числа тесно связаны со многими физическими явлениями. Они присутствуют в электромагнетизме, используются в электронике, электротехнике, квантовой механике и при изучении волн. В математической биологии комплексные числа применяются при изучении биологических ритмов, занимают важное место в теории хаоса, без них невозможно представить фракталы на компьютере.

Графическое представление комплексных чисел очень просто. Если предположить, что комплексное число — это точка z , то в декартовой системе координат, которую далее мы будем называть комплексной плоскостью, на горизонтальной оси X будет откладываться его вещественная часть а , на вертикальной оси Y — мнимая часть Ь .

Если мы также обозначим через r расстояние от начала координат до точки z , нетрудно показать, что это расстояние (оно называется модулем комплексного числа и обозначается | z |) равно √( a 2+ Ь 2). Более того, если учесть, что вещественная часть а равна косинусу угла α между осью х и радиус-вектором точки z , умноженному на модуль комплексного числа, а мнимая часть Ь — синусу угла α , умноженному на модуль комплексного числа, то в так называемых полярных координатах число z будет записываться следующим образом:

z = r ·(cos( α ) + i ·sin( α )).

Одно из самых любопытных свойств комплексных чисел заключается в том, что они расширяют возможности моделирования реальности, так как на них не распространяются ограничения, свойственные вещественным числам. Чтобы совершать с ними действия, можно представить, что, находясь на комплексной плоскости, ученый одной ногой стоит в вещественном мире (ему соответствует часть а ), другой — в мнимом мире (ему соответствует часть b ). При необходимости он беспрепятственно путешествует из одного мира в другой. Таким образом, к примеру, операции сложения и умножения комплексных чисел расширяют значение этих двух операций, что вы могли видеть при изучении фракталов Мандельброта и множеств Жюлиа.

С комплексными числами могут выполняться операции сложения и вычитания. На первый взгляд это кажется сложным, но в действительности это не так. Сумма двух комплексных чисел а + bi и с + di рассчитывается следующим образом:

( а + i ) + ( с + di ) = ( а + с ) + ( b + d ) i .

К примеру, (2 + 5 i ) + (3 — i ) = (2 + 3) + (5–1) i = 5 + 4 i .

Вычитание — операция, обратная сложению, следовательно, разность комплексных чисел a + bi и с + di рассчитывается так:

( а + i ) + ( с + di ) = ( а — с ) + ( b — d ) i .

К примеру, (1 + 3 i ) — (4 + 2 i ) = (1–4) + (3–2) i = —3 + i .

Также для комплексных чисел определены умножение и деление.

Произведение двух комплексных чисел а + bi и с + di определяется так:

( а + bi )·( с + di ) = ( ас — bd ) + ( ad + bc ) i .

Обратите внимание, что результат умножения можно получить следующим, более понятным способом:

( а + bi )·( с + di ) = а · с + а · d · i + b · с · i + b · d · i 2.

Напомним, что i 2= —1. Имеем:

a · c + a · d · i + b · i · c — b · d .

Приведем подобные слагаемые:

( ас — bd ) + ( ad + bc ) i .

К примеру, (2 + 6 i )·(8 + 2 i ) = (2·8–6·2) + (2·2 + 6·8) i = 4 + 52 i .

Частное двух комплексных чисел а + bi и с + di определяется так:

Например,

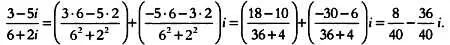
И вновь обратите внимание, что частное двух комплексных чисел — это результат выполнения следующей последовательности действий:

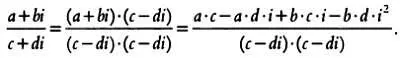
Приведем подобные слагаемые:

Комплексные числа полезны не только для графического изображения фракталов. Их постоянно используют инженеры при работе с электрическими цепями. Так, мощность бытовой техники выражается вещественными числами, мощность промышленных устройств — комплексными. Изучение биологических циклов, которые переживает человек, и анализ колебаний (к примеру, колебаний тела, закрепленного на пружине) в физике отчасти схожи: для решения этих задач используются комплексные числа. По этой причине те, кто знаком с комплексными числами, обычно используют формулу, которая считается одной из самых красивых и полезных в математике. Это формула Эйлера, связывающая мнимую единицу i , степень числа е и тригонометрические функции синуса и косинуса: