Рафаэль Лаос-Бельтра - Том 28. Математика жизни. Численные модели в биологии и экологии.

Существуют ли квадратные корни из отрицательных чисел? Утвердительный ответ на оба этих вопроса дали итальянские математики Джероламо Кардано и Рафаэль Бомбелли в середине XV века. Найденные ими числа названы мнимыми. С того времени из соображений удобства мнимая единица обозначается буквой i. Ее значение равно i= √—1 или, что аналогично, i 2 = -1. На основе мнимой единицы были определены так называемые комплексные числа. Ученые и инженеры используют их в самых разных областях с той же легкостью, с какой мы в повседневной жизни применяем 10, 23, 6, 1/2 и т. д. Комплексные числа состоят из двух частей — вещественной аи мнимой Ь. К примеру, комплексными являются 3 + 2 i, 6 + 7 i, и т. д. В стандартной форме они записываются в виде а+ bi(обратите внимание, что аи b— вещественные числа). По-настоящему удивительно то, что комплексные числа находят широкое применение в биологии, инженерном деле, прикладной математике и т. д. Подробнее о действиях с ними рассказано в приложении.

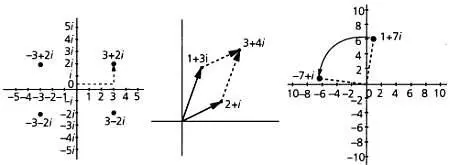
Слева — представление комплексных чисел. На оси Xоткладывается вещественная часть, на оси Y— мнимая. В центре представлена сумма двух комплексных чисел (1 + 3 i) + (2 + i), справа — произведение (1 + 7 i) и мнимой единицы i.

* * *

Природа состоит из неодушевленных предметов (облаков, гор, побережий, снежинок), живых организмов (растений, микроорганизмов, водорослей, кораллов) и их структур (бронхиальной системы, кровеносной системы или нейронных сетей), в которых снова и снова повторяется один и тот же узор. На каком бы уровне ни производились наблюдения, в любом масштабе (на расстояниях порядка нескольких метров, сантиметров и даже миллиметров) существует некая повторяющаяся схема. Подобные структуры, обладающие самоподобием, называются фракталами.

Основная идея проста: природа выстраивает структуры, следуя принципу наименьших затрат, а затем этот шаблон или образец повторяется в разном масштабе. Классический пример — ветвление растений. Нетрудно видеть, что отдельная большая ветвь и отходящие от нее мелкие ветви есть не что иное, как уменьшенная версия всего растения в целом.

Ветвление растений — пример фрактальной структуры в природе.

Сегодня считается, что температура здорового тела, дыхательный ритм и артериальное давление подобны фракталам. Если мы будем измерять температуру тела и артериальное давление каждые десять минут, раз в неделю или в месяц, а затем представим данные графически, построенный график будет обладать самоподобием. Но во время заболевания самоподобие на графиках не наблюдается. Заболевание — это утрата системой сложности, когда физиологические переменные перестают описываться фракталами.

Другой пример — электроэнцефалограмма человека. Ее аттрактор также имеет фрактальную природу. Размерность аттрактора D (о понятии размерности поговорим чуть позже) будет неким числом. С точки зрения нейрофизиологии по-настоящему интересно то, что значение D зависит от состояния человека и отличается у здоровых людей в состоянии бодрствования, здоровых людей, находящихся под воздействием анестезии, и у эпилептиков.

Какие свойства фракталов делают их столь интересными? Их размерность не выражается целым числом, а мы к этому привыкли в нашем мире, который математики называют евклидовым. Так, лист бумаги имеет длину и ширину, поэтому его размерность D равна 2. Если мы проведем прямую линию на листе бумаги, ее размерность D будет равна 1. Комната, в которой стоит стол, на котором лежит лист бумаги, на котором мы провели линию, имеет длину, ширину и высоту. Это означает, что комната имеет три измерения, и ее размерность D = 3. Говоря, что размерность фракталов не выражается целыми числами, мы имеем в виду, что их размерность D равна 1,8, 2,6 или другим подобным значениям.

Еще фракталы бесконечны: независимо от масштаба наблюдений кажется, что они никогда не заканчиваются. С помощью компьютерных программ Fractint или Ultra Fractal можно убедиться, что увеличивать определенный участок фрактала можно до бесконечности. Во время эксперимента вы также увидите, что фракталы обладают самоподобием, иными словами, вам будет казаться, что вы постоянно видите один и тот же узор, который проявляется во всей красоте и сложности и не изменяется в зависимости от масштаба наблюдений.

* * *

ИЗОБРАЖЕНИЕ ФРАКТАЛОВ НА КОМПЬЮТЕРЕ

Одна из классических компьютерных программ для изображения фракталов называется Fractint. Существуют ее версии для Windows, Linux и Mac OS. Одна из самых интересных особенностей программы — широкие возможности увеличения изображений: она позволяет просматривать фракталы с точностью до 1600 знаков после запятой. Несомненно, это одно из лучших приложений с точки зрения мощности алгоритмов и математической точности.

В подобных программах важен набор доступных инструментов. К примеру, программа Ultra Fractal позволяет изменять цвета фракталов, использовать слои и маски, генерировать анимации и т. д. Используя слои, вы сможете объединить несколько фракталов и получить поистине прекрасный рисунок. Также следует отметить программу Aphysis, предназначенную для изображения «туманных» фракталов. Она создана Марком Таунсендом и позволяет на основе заранее определенных фракталов генерировать их вариации. Некоторые приложения отличаются особым обилием настроек. К примеру, Fractal Explorer содержит 148 классов фракталов и позволяет создавать странные аттракторы (аттракторы в 3D), включает системы итерируемых функций и 22 класса так называемых кватернионов. Кроме того, в этой программе можно генерировать спецэффекты с помощью 117 фильтров, она содержит 12 алгоритмов выбора цвета, поддерживает создание анимаций в формате AVI и т. д. Интересный компонент приложения — FEParser (© Kyle McCord) — компилятор формул, ориентированный на продвинутых пользователей, с помощью которого можно создавать собственные фракталы. Другие программы, например XenoDream, выделяются благодаря художественной составляющей. Они позволяют добавлять текстуры и эффекты освещения, создавать фракталы в 3D, анимации и стереограммы. Мы упомянули лишь некоторые из множества приложений, предназначенных для решения самых разных задач, от генерации интересных картинок до математического изучения фракталов или создания на их основе настоящих произведений искусства.