Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— А все-таки, наверно, трудно… — грустно заметил Илюша.

— Не очень! Конечно, поскольку само кубическое уравнение сложнее квадратного, то весь ход решения похитрей. Но тут дело в том, что выясняются некоторые особые подробности… Итак, у нас имеется кубическое уравнение, где коэффициент при старшем члене уже превращен в единицу:

х 3+ ах 2+ bх + с = 0.

Цель снова будет та же самая: придумать такие преобразования, чтобы превратить данное уравнение в уравнение с меньшим числом членов, ибо, как мы видели на примере квадратного, этот прием упрощает задачу. Сперва мы будем поступать так же, как с квадратным уравнением. Положим снова:

х = у + h

и подставим это в наше уравнение. Получим после небольших переделок

у 3+ (3 h + а ) у 2+ (3 h 2+ 2 ah + b ) у + h 3+ ah 2+ bh + с = 0.

Теперь снова постараемся обратить коэффициент второго члена (при игреке в квадрате) в нуль, то есть положим, что

(3 h + a ) = 0; h = — a /3,

откуда

у 3+ (—3 a /3 + а ) у 2+ (3 a 2/9 — 2 a 2/3 + b ) у + h 3+ ah 2+ bh + с = 0.

— 432 —

или, сделав приведение:

у 3+ (— a 2/3 + b ) у + (2 a 3/27 — ab /3 + с ) = 0.

Теперь для сокращения письма положим:

(— a 2/3 + b ) = p ; (2 a 3/27 — ab /3 + с ) ] = q

и запишем окончательно результат в таком виде:

y 3+ py + q = 0.

(Если q = 0, то все просто: y 1= 0, у 2,3= ±√— p )

При q ≠ 0 результат, как ты видишь, разумеется, несколько менее утешителен, чем в случае квадратного уравнения, ибо у нас не два, а три члена. Но как-никак определенное упрощение достигнуто. Как же теперь быть далее? Ясно, что нужно придумать способ, который дал бы возможность обратить выражение ру в нуль, после чего мы и получим двучленное уравнение, то есть то же самое, что было получено для квадратного. И вот как раз на этом месте болонцам пришла в голову счастливая мысль сделать еще одну подстановку: положить, что у в последнем уравнении можно представить в виде суммы:

у = u + v .

И опять-таки эти величины ими пока что совершенно произвольные. Мы только одно можем сказать, что сумма их есть корень нашего уравнения, который не равен нулю.

— А почему он не равен нулю?

— Сейчас рассмотрим! Попробуем подставить. Получаем:

( u + v ) 3+ р ( u + v ) + q = 0.

Смотрите-ка! Теперь видно, что сумма ( u + v ) не может быть равна нулю, потому что тогда и число q будет равно нулю, а число q , свободный член уравнения, не равно нулю. Теперь откроем скобки и кое-что сгруппируем:

( u 3+ v 3) + ( u + v ) (3 uv + p ) + q = 0.

Такая форма уравнения уже подает нам некоторые надежды! Может быть, нам удастся уничтожить второй член? Положить,

— 433 —

что u + v = 0, мы, как сказано, не можем, но зато спокойно можем допустить, что

3 uv + р = 0;

uv = — p /3

но в таком случае наше уравнение превращается в такое:

u 3+ v 3= — q.

Следовательно, мы получили два уравнения. Одно из них дает произведение новых чисел uи v, а другое их сумму. Правда, они в разных степенях, но никто не помешает возвести это произведение тоже в куб. Далее это создаст нам некоторые затруднения, но мы как-нибудь их одолеем. И вот перед нами два уравнения:

u 3 v 3= — p 3/27; u 3+ v 3= — q .

А теперь скажите, юноша, как бы вы дальше поступили с этими уравнениями? Отвечайте, куда они просятся?

— В квадратное уравнение! — вдруг выпалил почти в отчаянии Илюша. — Сумма и произведение даны, значит, это квадратное уравнение… по теореме Виеты.

— Очень хорошо! — отозвался Мнимий. — Так вот: теперь должно быть ясно, что болонцы действительно напали на очень счастливую мысль. Разумеется, им не удалось свести кубическое уравнение к линейному (то есть первой степени), как сводили квадратное, но ведь этого и ожидать было бы странно, ибо куб все-таки постарше квадрата и, конечно, поупрямей его! Но вы должны еще иметь в виду, что открытие этого решения кубического уравнения в Италии шестнадцатого века было поистине важным историческим событием! Оно означало, что новая Европа вышла на новый рубеж, она уже освоила наследие древних ученых и теперь сама делает недоступные для древности открытия. Общественные условия настолько изменились, что возникла возможность для новой науки. Разумеется, ученый работает прежде всего в интересах науки. Но он может работать для ее развития только тогда, когда общество, в котором он живет, поддерживает его, другими словами, когда люди верят в необходимость его трудов. Мы уже говорили с вами, как бились древние греки с двоекубием, то есть задачей удвоить куб. И как мы увидим далее, задача трисекции угла тоже сводится к кубическому уравнению. Но так или иначе болонцы все-таки степень кубического уравнения на единицу понизили, а это облегчило задачу — квадратные уравнения мы решать умеем!

— Вавилоняне догадались, — заметил Радикс, — да и нас научили.

— 434 —

— И теперь уже мы можем составить окончательное уравнение, которое будет:

t 2+ qt — p 3/27 = 0

Одно значение корня этого уравнения даст u 3, а другое v 3. Решим это уравнение!

Илюша схватил мел и сразу написал:

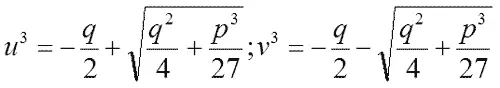
— Вот-вот, — поддакнул Мнимий, — совершенно правильно. На пятерку! Но теперь, поскольку мы знаем, что у = u + v , пишите уж и самое решение.

И наш герой написал следующее:

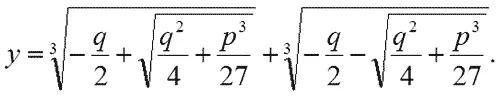
— Ну вот, — произнес Мнимий, — и появилась эта знаменитая формула Кардана для решения кубического уравнения.