Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— 444 —

Трисекция Гиясэддина ал-Каши.

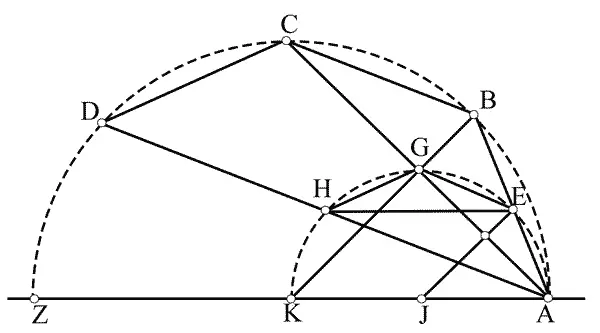
Хорды — двойные синусы. По теореме Птолемея (если четыре вершины четырехугольника лежат на окружности, сумма произведений противоположных сторон равна произведению диагоналей), из четырехугольника AEGH, АЕ = EG = GH и EH = AG , выводим, что AG 2= АЕ 2+ АЕ · АН . По теореме Евклида (произведение отрезков хорды равно произведению отрезков диаметра, проходящего через точку пересечения диаметра с хордой), так как AG = GC , получаем AG 2= BG (2 R— BG ), где R — радиус большого круга; затем но теореме Пифагора из треугольника ABG выводим: AG 2= 4 AE 2 — (4 AE 4: R 2).

Приравнивая два выражения для AG , получаем: АЕ 2+ AЕ · АН = 4 АЕ 2— (4 АЕ 4: R 2). Полагая, что АЕ = sin а и что АН = sin З а (ибо хорда АН стягивает утроенную дугу), а R = 1, получаем для любого угла выражение 3 sin а — 4 sin 3 a = sin З а .

Благодаря этому построению замечательные самаркандские математики в XV веке сумели вычислить синус одного градуса с восемнадцатью точными знаками после запятой.

вым математиком, одним из последних ученых исламитского мира, который трудился у знаменитого астронома Улугбека в Самарканде в пятнадцатом веке. Работы Улугбека были уничтожены реакционным духовенством, его обсерватория разрушена, а сам он был убит. Но память о работах ученых его школы осталась, и в шестнадцатом веке Мариам Челеби, внук ар-Руми, астронома, работавшего вместе с Улугбеком, обнародовал решение задачи трисекции угла. В Европе это решение узнали только в девятнадцатом веке. Это решение не дает искомого угла построением, как невсис Паппа. Но при его помощи можно получить нужное кубическое уравнение.

— 445 —

— А как потом решали кубические уравнения?

— К этому труднейшему вопросу вернулись через некоторое время. Сначала Эйлер со свойственной ему наблюдательностью заметил, что по формуле Кардана получается девять значений корней, тогда как ясно, что нужны всего три. И Эйлер показал, как надо комбинировать между собой эти значения, чтобы получить те три, которые нужны. Таким образом выяснилось, что в формуле Кардана таится еще один неожиданный секрет.

— А почему девять значений? — удивился Илюша.

— Да ведь в формуле Кардана два кубических корня, у каждого три значения, и если каждое из трех значений первого комбинировать с тремя значениями второго…

— … то и получим девять! — заключил мальчик. — А как их комбинировать?

— У вас ведь есть уравнение:

uv = — p /3

так вот мы и должны так их соединять, чтобы их произведение давало бы как раз эту величину, то есть — у. Это как раз и заметил Эйлер. Однако вскоре выяснилось, что можно действовать еще и другим способом, очень интересным…

— Как это так?

— Все это можно сделать, опираясь на важные положения, касающиеся извлечения корней из комплексных чисел. Эта операция не очень проста. Она делается при помощи так называемых корней из единицы…

— Не совсем понимаю, — перебил Илья, — запутался!..

— Ничего, смелее! Допустим, что мы извлекаем из комплексного числа корень пятой степени. Переходим к тригонометрической форме комплексного числа и пишем:

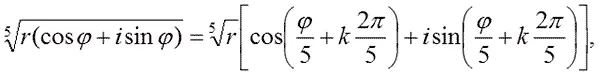
где к = 0, 1, 2, 3, 4, как мы уже это выяснили ранее. Но когда мы перемножаем комплексные числа, углы, вернее, аргументы комплексных чисел складываются и ничто не мешает суммы аргументов разъединить и написать извлечение корня пятой степени в таком виде:

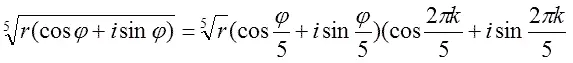
— 446 —

Отсюда вытекает утверждение, что все значения корня из комплексного числа можно получить, умножая одно из этих значении на разные значения корпя той же степени из единицы, то есть на вторую скобку правой части. Представляете себе?

— Кажется, теперь представляю, — осторожно признался Илья. — Только разве это так важно, написать в таком виде, а не в другом?

— В таком кропотливом деле, как это, — отвечал Мнимий, — нельзя пренебрегать ни малейшим упрощением. Так и в данном случае, то есть для куба, при решении уравнения

x 3= 1

Первый корень, конечно, равен единице, а другие два…

— Другие два, — подсказал Илюша, — получаются из квадратного уравнения, то есть из такого:

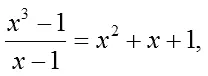
где в правой части неполный квадрат суммы. Решая квадратное уравнение, получаем:

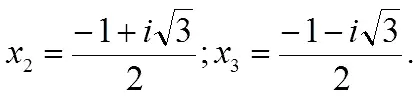
— Правильно… — заметил Мнимий. — Но давайте проделаем еще один поучительный опыт: возведем наш только что полученный икс-второй в квадрат:

— И получился, — сказал Илья, — не кто иной, как сам икс-третий! Ну, а если его еще и в куб?.. Правильно! Единица получается. Все в порядке.

— Так вот, — продолжал Мнимий, — назовем один из корней из единицы, то есть наш икс-второй, греческой буквой альфа. Тогда икс-третий, как вы только что выяснили, будет а 2. А теперь я должен еще отметить, что среди всех корней из единицы (для квадратного корня два, для кубического три, и так далее, то есть их число совпадает с числом единиц в показателе корня) имеются такие корни, которые обладают весьма интересным и полезным свойством. Если мы один из таких корней будем возводить последовательно в возрастаю-

— 447 —

щие степени, начиная со второй, то получим все остальные корни данной совокупности. Например, второй и третий корни кубические из единицы (первый, конечно, единица) обладают этим свойством, так что

а 2 2= а 3; а 3 2= а 2; а 2 3= а 1= 1.

Если же взять для другого примера все корни шестой степени из единицы, от а 1до а 6, то из них только два (а именно а 1и а 5) обладают этим свойством и называются первообразными корнями. Например, из корней четвертой степени первообразных только два ( a 2и а 4), тогда как для пятой степени все корни, не считая первого, равного 1, будут первообразными. Если вписать в единичный круг правильный многоугольник, одна вершина которого лежит в точке с координатами 1, 0), то можно заметить, что только те его вершины будут давать первообразные корни, которые принадлежат именно этому многоугольнику, но отнюдь не какому-либо другому — с меньшим числом сторон и одной вершиной к точке с координатами A, 0). Прошу покорнейше запомнить это правило. Оно нетрудное. А теперь мы можем снова перейти и к формуле Кардана. Если у нас есть уравнение кубическое: